题目内容
 如图是函数f(x)=Asin(ωx+φ)(x∈R)在区间[
如图是函数f(x)=Asin(ωx+φ)(x∈R)在区间[| π |
| 6 |
| 7π |
| 6 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向左平移
| ||||
D、向左平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由函数图象得到f(x)=Asin(ωx+φ)的解析式,然后直接利用函数图象的平移得答案.
解答:
解:由图可知,A=1,T=
=π,
∴ω=2.
由五点作图的第一点知,2×
+φ=0,得φ=-
.
则f(x)=sin(2x-
).
∴需把函数g(x)=sinx(x∈R)的图象上所有的点向右平移
个单位,再把所得各点的横坐标缩短到原来的
倍,纵坐标不变得f(x)=sin(2x-
)的图象.
故选:B.
| 2π |
| ω |
∴ω=2.
由五点作图的第一点知,2×
| π |
| 6 |
| π |
| 3 |
则f(x)=sin(2x-
| π |
| 3 |
∴需把函数g(x)=sinx(x∈R)的图象上所有的点向右平移
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
故选:B.
点评:本题考查了由y=Asin(ωx+φ)的部分图象求函数解析式,考查了三角函数的平移.三角函数的平移原则为左加右减上加下减,是基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
一个简单几何体的正视图、俯视图如图所示,则其侧视图不可能是( )
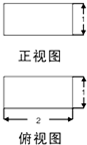

| A、正方形 | B、直角梯形 |
| C、等腰三角形 | D、圆 |
设集合M={x|x>1},N={x|x2>1},则下列关系中正确的是( )
| A、M=N | B、M∪N=N |
| C、M∪N=M | D、M∩N=N |
在复平面内,复数
+(1+i)2对应的点位于( )
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若M点的极坐标为(-2,-
),则M点的直角坐标是( )
| π |
| 6 |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
已知变量x,y满足约束条件
,则z=2x+y的最大值是( )
|
| A、-3 | ||
B、
| ||
| C、3 | ||
| D、5 |
设随机变量ξ服从正态分布N(0,1),P(ξ>1)=p,则P(-1<ξ<0)等于( )
A、
| ||
| B、1-p | ||
| C、1-2p | ||
D、
|
如果复数(1+bi)(2+i)是纯虚数,则|
|的值为( )
| 2b+3i |
| 1+bi |
| A、2 | ||
B、
| ||
| C、5 | ||
| D、15 |