题目内容
由函数y=x2的图象与直线x=1、x=2和x轴所围成的封闭图形的面积是( )
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:确定积分区间,然后根据积分的运算公式进行求解即可.
解答:
解:由y=x2的图象与直线x=1、x=2和x轴所围成的封闭图形的面积,
就是:
x2dx=
x3
=
故选:B.
就是:
| ∫ | 2 1 |
| 1 |
| 3 |
| | | 2 1 |
| 7 |
| 3 |
故选:B.
点评:利用定积分求封闭图形的面积是求面积的通法,应熟练掌握.

练习册系列答案
相关题目
已知直角坐标系xoy中,直线的参数方程为
(t为参数).以直角坐标系xOy中的原点O为极点,x轴的非负半轴为极轴,圆C的极坐标方程为ρ2-6ρcosθ+5=0,则圆心C到直线距离为 .
|
已知x,y∈R,i为虚数单位,且x+yi=
,则x+y=( )
| 3+4i |
| 1+2i |
A、
| ||
B、
| ||
C、
| ||
D、
|
当0≤x≤
时,|ax-2x3|≤
恒成立,则实数a的取值范围是( )
| 1 |
| 2 |
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、a≥-
| ||||
D、a≤
|
已知直线l的参数方程为
(t为参数),则直线l的普通方程为( )
|
| A、x-y-2=0 |
| B、x-y+2=0 |
| C、x+y=0 |
| D、x+y-2=0 |
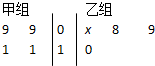 如图,茎叶图记录了甲、乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.若甲、乙两组共有8名同学植树棵数的平均数为9,则x为( )
如图,茎叶图记录了甲、乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.若甲、乙两组共有8名同学植树棵数的平均数为9,则x为( )