题目内容
下列函数中，既是偶函数又在（0，+∞）上单调递增的函数是（ ）
| A、y=2x3 |
| B、y=|x|+1 |
| C、y=-x2+4 |
| D、y=2-|x| |
考点：函数奇偶性的判断,函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：由函数的奇偶性和单调性的定义和性质，对选项一一加以判断，即可得到既是偶函数又在（0，+∞）上单调递增的函数．
解答：
解：对于A．y=2x3，由f（-x）=-2x3=-f（x），为奇函数，故排除A；
对于B．y=|x|+1，由f（-x）=|-x|+1=f（x），为偶函数，当x＞0时，y=x+1，是增函数，故B正确；
对于C．y=-x2+4，有f（-x）=f（x），是偶函数，但x＞0时为减函数，故排除C；
对于D．y=2-|x|，有f（-x）=f（x），是偶函数，当x＞0时，y=2-x，为减函数，故排除D．
故选B．
对于B．y=|x|+1，由f（-x）=|-x|+1=f（x），为偶函数，当x＞0时，y=x+1，是增函数，故B正确；
对于C．y=-x2+4，有f（-x）=f（x），是偶函数，但x＞0时为减函数，故排除C；
对于D．y=2-|x|，有f（-x）=f（x），是偶函数，当x＞0时，y=2-x，为减函数，故排除D．
故选B．
点评：本题考查函数的性质和运用，考查函数的奇偶性和单调性及运用，注意定义的运用，以及函数的定义域，属于基础题和易错题．
练习册系列答案
相关题目
下列命题中，假命题是（ ）
| A、?x∈R，2x-1＞0 | ||
B、?x∈R，sinx=
| ||
| C、?x∈R，x2-x+1＞0 | ||
| D、?x∈R，lgx=2 |
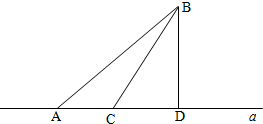如图，某海滨浴场的岸边可近似地看作直线a，救生员现在岸边的A处，发现海中的B处有人求救，救生员没有直接从A处游向B处，而是在AD（D为海岸边距B最近的点）上找到一点C，沿岸边从A处跑到C处，然后游到B处，若救生员在岸边的行进速度为4（m/s），在海水中的行进速度为2（m/s），∠BAD=45°，BD=200（m），救生员从A到C再到B的时间为y（s）．已知(
)a＞(
)b，则a，b的大小关系是（ ）
| 2 |
| 2 |
| A、1＞a＞b＞0 |
| B、a＜b |
| C、a＞b |
| D、1＞a＞b＞0 |
若函数f（x）为奇函数，且当x＞0时f（x）=lgx，则f（-100）的值是（ ）
| A、-2 | ||
B、
| ||
| C、2 | ||
D、-
|
设全集为R，集合A={x||x|≥1}，则∁RA=（ ）
| A、[-1，1] |
| B、（-1，1） |
| C、（-∞，1） |
| D、（-∞，-1）∪（1，+∞） |