题目内容
已知F1、F2是双曲线
-
=1的左、右焦点,P为双曲线上一点,若PF1⊥F1F2,则线段PF1的长度为( )
| x2 |
| 4 |
| y2 |
| 5 |
A、
| ||
B、
| ||
| C、5 | ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,c=3,代入
-
=1,即可求出线段PF1的长度.
| x2 |
| 4 |
| y2 |
| 5 |
解答:
解:由题意,c=3,代入
-
=1可得
-
=1,
∴y=±
,
∴线段PF1的长度为
,
故选:B.
| x2 |
| 4 |
| y2 |
| 5 |
| 9 |
| 4 |
| y2 |
| 5 |
∴y=±
| 5 |
| 2 |
∴线段PF1的长度为
| 5 |
| 2 |
故选:B.
点评:本题考查线段PF1的长度,考查双曲线的性质,比较基础.

练习册系列答案
相关题目
若集合A={y|y2+y>0,y∈R},B={y|y=sinx,x∈R},则A∪B=( )
| A、R | B、(0,1] |
| C、(-∞,1) | D、∅ |
已知a、b、c为正数,且a+b+c=2,则
+
+
的最小值为( )
| 1 |
| a |
| 4 |
| b |
| 9 |
| c |
| A、24 | B、18 | C、12 | D、8 |
下列各组对象能构成集合的有( )
(1)所有的正方体
(2)湛江市所有的大酒店
(3)所有的高中数学难题
(4)湛江一中所有的优秀学生
(5)一中印刷厂2012年生产的所有产品
(6)直角坐标平面坐标轴上所有的点.
(1)所有的正方体
(2)湛江市所有的大酒店
(3)所有的高中数学难题
(4)湛江一中所有的优秀学生
(5)一中印刷厂2012年生产的所有产品
(6)直角坐标平面坐标轴上所有的点.
| A、(1)(2)(4) |
| B、(2)(3)(4) |
| C、(1)(5)(6) |
| D、(2)(4)(5) |
已知函数f(x)=
,则f(f(4))的值为( )
|
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
sin
的值等于( )
| 11π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
平行线3x-4y-3=0和6x-8y+5=0之间的距离是( )
A、
| ||
B、
| ||
C、
| ||
D、
|




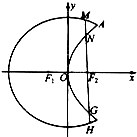 我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆