题目内容
数列{an}的前n项和为,且an是Sn和1的等差中项,bn等差数列.满足b1=a1,b4=S3
(1)求数列{an},{bn}的通项公式;
(2)设cn=
,数列{cn}的前n项和为Tn,若Tn≤λbn+1对一切n∈N*恒成立,求实数λ的最小值.
(1)求数列{an},{bn}的通项公式;
(2)设cn=
| 1 |
| bnbn+1 |
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(1)由题意可知,Sn=2an-1,结合递推公式a1=S1,n≥2时,an=Sn-Sn-1,可得an=2an-1,结合等比数列的通项公式可求由b1=a1=1,b4=1+3d=7,可求公差d,进而可求bn,
(2)由cn=
=
(
-
),利用裂项求和可求Tn,从而Tn≤λbn+1对一切n∈N*恒成立,可转化为
≤λ(2n+1)对一切n∈N*恒成立,结合数列的单调性,即可得出结论.
(2)由cn=
| 1 |
| bnbn+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
解答:
解:(1)∵an是Sn和1的等差中项,∴Sn=2an-1
当n=1时,a1=S1=2a1-1,∴a1=1.
当n≥2时,an=Sn-Sn-1=(2an-1)-(2an-1-1)=2an-2an-1,
∴an=2an-1,∴数列{an}是以a1=1为首项,2为公比的等比数列,
∴an=2n-1,Sn=2n-1.
设{bn}的公差为d,b1=a1=1,b4=1+3d=7,∴d=2,
∴bn=1+(n-1)×2=2n-1;
(2)cn=
=
(
-
)
∴Tn=
(1-
+
-
+…+
-
)=
∵Tn≤λbn+1对一切n∈N*恒成立,
∴
≤λ(2n+1)对一切n∈N*恒成立,
∴λ≥
.
令f(n)=
,则f(n)单调递减,
∴λ≥
.
当n=1时,a1=S1=2a1-1,∴a1=1.
当n≥2时,an=Sn-Sn-1=(2an-1)-(2an-1-1)=2an-2an-1,
∴an=2an-1,∴数列{an}是以a1=1为首项,2为公比的等比数列,
∴an=2n-1,Sn=2n-1.
设{bn}的公差为d,b1=a1=1,b4=1+3d=7,∴d=2,
∴bn=1+(n-1)×2=2n-1;
(2)cn=
| 1 |
| bnbn+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
∵Tn≤λbn+1对一切n∈N*恒成立,
∴
| n |
| 2n+1 |
∴λ≥
| 1 | ||
4n+
|
令f(n)=
| 1 | ||
4n+
|
∴λ≥
| 1 |
| 9 |
点评:本题主要考查了等差数列与等比数列的通项公式的应用,数列的递推公式的应用及数列的裂项求和及数列的单调性在数列的最值求解中的应用,难度中等.

练习册系列答案
相关题目
 已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD.
已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD.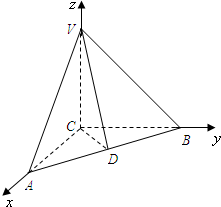 如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.
如图,在三棱锥V-ABC中,顶点C在空间直角坐标系的原点处,顶点A、B、V分别在x、y、z轴上,D是AB的中点,且AC=BC=2,∠VDC=θ.