题目内容
20.已知实数x,y满足方程x2+y2=3,求$\frac{y+1}{x+3}$的范围.分析 设B(x,y)为圆x2+y2=3上一点,A(-3,-1).由直线的斜率公式得m=$\frac{y+1}{x+3}$是直线AB的斜率,因此作出图形并加以观察,根据直线与圆的位置关系建立关系式求出m的最大、最小值,即得m的取值范围.
解答 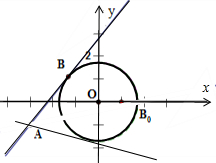 解:根据题意,可得
解:根据题意,可得
设A的坐标为(-3,-1),B(x,y)为圆x2+y2=3上一点,
令m=$\frac{y+1}{x+3}$,∴m可看作直线AB的斜率,
作出图形,当直线AB与圆相切时,m达到最值;
m=$\frac{y+1}{x+3}$可得y+1=mx+3m,即mx-y+3m-1=0.
直线与圆相切,可得$\sqrt{3}$=$\frac{|3m-1|}{\sqrt{1+{m}^{2}}}$,
解得:m=$\frac{3±\sqrt{21}}{6}$
则$\frac{y+1}{x+3}$的范围为[$\frac{3-\sqrt{21}}{6}$,$\frac{3+\sqrt{21}}{6}$].
点评 本题着重考查了直线的斜率、圆的方程、直线与圆的位置关系,考查转化思想以及数形结合的应用,属于中档题.

练习册系列答案
相关题目
5.有一个几何体的三视图及其尺寸如图单位(cm),则该几何体的表面积及体积为( )
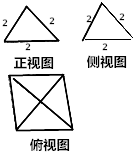

| A. | 4+4$\sqrt{3}$cm2,$\frac{16\sqrt{3}}{3}$cm3 | B. | 4+4$\sqrt{3}$cm2,$\frac{16\sqrt{2}}{3}$cm3 | C. | 12cm2,$\frac{16\sqrt{3}}{3}$cm3 | D. | 12cm2,$\frac{16\sqrt{2}}{3}$cm3 |
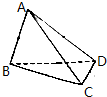 已知正四面体ABCD,点E,F分别为AB,CD的中点,边长为2.
已知正四面体ABCD,点E,F分别为AB,CD的中点,边长为2.