题目内容
10.化简下列各式(1)$\frac{\sqrt{3}cos(α+30°)-cos(α+120°)}{cos(a-10°)cos10°+cos(α+80°)cos80°}$.
(2)$\frac{2cos40°+cos10°(1+\sqrt{3}tan10°)}{sin50°cos35°+cos50°cos55°}$.
分析 (1)利用余弦加法定理、三角函数恒等式求解.
(2)利用三角函数恒等式、正弦函数加法定理、同角三角函数关系式能求出结果.
解答 解:(1)$\frac{\sqrt{3}cos(α+30°)-cos(α+120°)}{cos(a-10°)cos10°+cos(α+80°)cos80°}$
=$\frac{\sqrt{3}×\frac{\sqrt{3}}{2}cosα-\sqrt{3}×\frac{1}{2}sinα+\frac{1}{2}cosα+\frac{\sqrt{3}}{2}sinα}{cosαco{s}^{2}10°+sinαsin10°cos10°+cosαco{s}^{2}80°-sinαsin80°cos80°}$
=$\frac{2cosα}{cosα}$
=2.
(2)$\frac{2cos40°+cos10°(1+\sqrt{3}tan10°)}{sin50°cos35°+cos50°cos55°}$
=$\frac{2cos40°+cos10°(1+\sqrt{3}×\frac{sin10°}{cos10°})}{sin(50°+35°)}$
=$\frac{2cos40°+cos1{0°+\sqrt{3}sin10°}^{\;}}{cos5°}$
=$\frac{2cos40°+2sin40°}{cos5°}$
=$\frac{2\sqrt{2}sin8{5°}^{\;}}{cos5°}$
=2$\sqrt{2}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意余弦加法定理、三角函数恒等式、正弦函数加法定理、同角三角函数关系式的合理运用.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
20.若全集U={0,1,2,3,4,5},M={0,1},则∁UM=( )
| A. | {0,1} | B. | {2,3,4,5} | C. | {0,2,3,4,5} | D. | {1,2,3,4,5} |
1.已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设函数H1(x)=$\left\{\begin{array}{l}{f(x),f(x)≥g(x)}\\{g(x),f(x)<g(x)}\end{array}\right.$,H2(x)=$\left\{\begin{array}{l}{g(x),f(x)≥g(x)}\\{f(x),f(x)<g(x)}\end{array}\right.$,记H1(x)的最小值为A,H2(x)的最大值为B,则A-B( )
| A. | 16 | B. | -16 | C. | a2+2a-16 | D. | a2-2a-16 |
18.已知复数$z=\frac{5+3i}{1-i}$,则下列说法正确的是( )
| A. | z的虚部为4i | B. | z的共轭复数为1-4i | ||
| C. | |z|=5 | D. | z在复平面内对应的点在第二象限 |
2.过点($\sqrt{3}$,-1)且与圆x2+y2=4相切的直线方程是( )
| A. | $\sqrt{3}$x+y-4=0 | B. | x-$\sqrt{3}$y-4=0 | C. | x-$\sqrt{3}$y-2=0 | D. | $\sqrt{3}$x-y-4=0 |
20.与圆(x-2)2+y2=1相切且在两坐标轴上截距相等的直线共有( )
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 6条 |
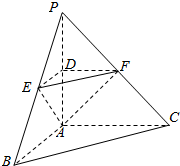 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥BC,AB⊥AC,PA=1,BC=2.D、E、F分别是棱PA、PB、PC的中点,连接DE、DF、EF.
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥BC,AB⊥AC,PA=1,BC=2.D、E、F分别是棱PA、PB、PC的中点,连接DE、DF、EF.