题目内容
已知函数f(x)的定义域为(4a-3,3-2a2),a∈R,且y=f(2x-3)是偶函数,又g(x)=x3+ax2+
+
,存在x0∈(k,k+
),k∈Z,使得g(x0)=x0,则满足条件的实数k的个数为( )
| x |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| A、3 | B、2 | C、4 | D、1 |
考点:函数奇偶性的性质
专题:计算题,作图题,函数的性质及应用
分析:令2x1-3=4a-3,2x2-3=3-2a2,再由y=f(2x-3)是偶凼数可得a=-1;从而令h(x)=x3-x2-
+
,从而由零点的判定定理求解.
| x |
| 2 |
| 1 |
| 4 |
解答:
 解:令2x1-3=4a-3,2x2-3=3-2a2,
解:令2x1-3=4a-3,2x2-3=3-2a2,
从而可得,x1=2a,x2=3-a2,
故3-a2+2a=0;
解得,a=3或a=-1;
当a=3时,4a-3=9,3-2a2=-9;
不成立;
当a=-1时,成立;
令h(x)=x3-x2-
+
,
h′(x)=3x2-2x-
=3(x-
)(x-
);
且h(-1)=-1-1+
+
<0,
h(-
)=-
-
+
+
=
>0;
h(0)=
>0,h(
)=
-
-
+
=-
<0;
h(1)=1-1-
+
<0,h(
)=
-
-
+
=
>0;
从而可知,k可以取-1,0,1三个数,
故选A.
 解:令2x1-3=4a-3,2x2-3=3-2a2,
解:令2x1-3=4a-3,2x2-3=3-2a2,从而可得,x1=2a,x2=3-a2,
故3-a2+2a=0;
解得,a=3或a=-1;
当a=3时,4a-3=9,3-2a2=-9;
不成立;
当a=-1时,成立;
令h(x)=x3-x2-
| x |
| 2 |
| 1 |
| 4 |
h′(x)=3x2-2x-
| 1 |
| 2 |
2-
| ||
| 6 |
2+
| ||
| 6 |
且h(-1)=-1-1+
| 1 |
| 2 |
| 1 |
| 4 |
h(-
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
h(0)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
h(1)=1-1-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 27 |
| 8 |
| 9 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 5 |
| 8 |
从而可知,k可以取-1,0,1三个数,
故选A.
点评:本题考查了导数的综合应用及零点的判定定理的应用,属于基础题.

练习册系列答案
相关题目
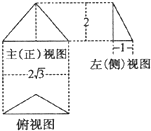 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的四个表面中,面积的最大值为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的四个表面中,面积的最大值为