题目内容
5.曲线C是平面内与两个定点F1(-2,0),F2(2,0)的距离之积等于9的点的轨迹.给出下列命题:①曲线C过坐标原点;
②曲线C关于坐标轴对称;
③若点P在曲线C上,则△F1PF2的周长有最小值10;
④若点P在曲线C上,则△F1PF2面积有最大值$\frac{9}{2}$.
其中正确命题的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据定义求出曲线C的方程,根据方程特点判断①,②,根据基本不等式判断③,把y2看作x2的函数,解出y2,得出S=2y,求出y的范围即可得出S的范围.
解答 解:设曲线C上任意一点的坐标为P(x,y),则[(x+2)2+y2]•[(x-2)2+y2]=81,
①把x=0,y=0代入上式得1=81,故曲线C不经过原点,故①错误;
②把(-x,y)代入上式得[(-x+2)2+y2][(-x-2)2+y2]=[(x-2)2+y2][(x+2)2+y2]=81,
∴曲线C关于y轴对称,
把(x,-y)代入上式显然也成立,故曲线C关于x轴对称,故②正确;
③∵|PF1|+|PF2|≥2$\sqrt{|PF1|•|PF2|}$=2$\sqrt{9}$=6,
∴△F1PF2的周长为|PF1|+|PF2|+|F1F2|≥6+4=10,故③正确;
④△F1PF2面积S=$\frac{1}{2}×4×y$=2y,∴S2=4y2,
∵[(x+2)2+y2]•[(x-2)2+y2]=81,∴y4+(2x2+8)y2+(x2-4)2-81=0,
∴y2=$\sqrt{24{x}^{2}+81}$-x2-4或y2=-$\sqrt{24{x}^{2}+81}$-x2-4(舍).
设$\sqrt{24{x}^{2}+81}$=t,则x2=$\frac{{t}^{2}-81}{24}$,
∴y2=t-$\frac{{t}^{2}-81}{24}$-4=-$\frac{1}{24}$t2+t-$\frac{5}{8}$=-$\frac{1}{24}$(t-12)2+$\frac{43}{8}$,
∴当t=12时,y2取得最大值$\frac{43}{8}$,即S的最大值为2$\sqrt{\frac{43}{8}}$,故④错误.
故选C.
点评 本题考查了轨迹方程的求解,基本不等式及函数最值的计算,属于中档题.

| A. | 向右平行移动$\frac{5π}{12}$个单位长度 | B. | 向左平行移动$\frac{5π}{12}$个单位长度 | ||
| C. | 向右平行移动$\frac{5π}{6}$个单位长度 | D. | 向左平行移动$\frac{5π}{6}$个单位长度 |
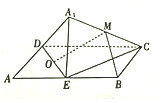 如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE(A1∉平面ABCD).若M、O分别为线段A1C、DE的中点,则在△ADE翻转过程中,下列说法错误的是( )| A. | 与平面A1DE垂直的直线必与直线BM垂直 | |
| B. | 过E作EG∥BM,G∈平面A1DC,则∠A1EG为定值 | |
| C. | 一定存在某个位置,使DE⊥MO | |
| D. | 三棱锥A1-ADE外接球半径与棱AD的长之比为定值 |
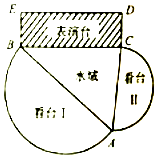 在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC,及矩形表演台BCDE四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以AB,AC为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,CD=10米,三角形水域ABC的面积为$400\sqrt{3}$平方米,设∠BAC=θ.
在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC,及矩形表演台BCDE四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以AB,AC为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,CD=10米,三角形水域ABC的面积为$400\sqrt{3}$平方米,设∠BAC=θ.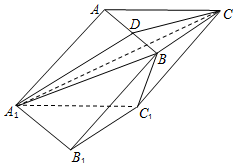 如图,在底边为等边三角形的斜三棱柱ABC-A1B1C1中,AA1=$\sqrt{3}$AB,四边形B1C1CB为矩形,过A1C做与直线BC1平行的平面A1CD交AB于点D.
如图,在底边为等边三角形的斜三棱柱ABC-A1B1C1中,AA1=$\sqrt{3}$AB,四边形B1C1CB为矩形,过A1C做与直线BC1平行的平面A1CD交AB于点D.