题目内容

9．已知直四棱柱底面是边长为2的菱形，侧面对角线的长为$2\sqrt{3}$，则该直四棱柱的侧面积为16$\sqrt{2}$．

分析 根据题意画出图形，结合图形求出侧棱长，再计算四棱柱的侧面积．

解答 解：如图所示，
直四棱柱底面ABCD是边长为2的菱形，
侧面对角线的长为$2\sqrt{3}$，
∴侧棱长为CC1=$\sqrt{{（2\sqrt{3}）}^{2}{-2}^{2}}$=2$\sqrt{2}$；
∴该直四棱柱的侧面积为S=4×2×2$\sqrt{2}$=16$\sqrt{2}$．
故答案为：16$\sqrt{2}$．

点评 本题考查了空间几何体的性质与面积的计算问题，是基础题．

练习册系列答案
相关题目
5．曲线C是平面内与两个定点F1（-2，0），F2（2，0）的距离之积等于9的点的轨迹．给出下列命题：
①曲线C过坐标原点；
②曲线C关于坐标轴对称；
③若点P在曲线C上，则△F1PF2的周长有最小值10；
④若点P在曲线C上，则△F1PF2面积有最大值$\frac{9}{2}$．
其中正确命题的个数为（　　）
A．0B．1C．2D．3
20．已知点A（-4，0），B（-1，0），C（-4，3），动点P、Q满足$\frac{|PA|}{|PB|}$=$\frac{|QA|}{|QB|}$=2，则|$\overrightarrow{CP}$+$\overrightarrow{CQ}$|取值范围是 （　　）
A．[1，16]B．[6，14]C．[4，16]D．[$\sqrt{13}$，3$\sqrt{5}$]
17．已知函数f（x）=（ax-1）e2x+x+1（其中e为自然对数的e底数）．
（Ⅰ）若a=0，求函数f（x）的单调区间；
（Ⅱ）对?x∈（0，+∞），f（x）＞0恒成立，求a的取值范围．
4．已知i是虚数单位，复数z1=3+yi（y∈R），z2=2-i，且$\frac{z_1}{z_2}=1+i$，则y=1．
14．已知向量$\overrightarrow m=（{\sqrt{3}cosx，-1}），\overrightarrow n=（{sinx，{{cos}^2}x}）$．
（1）当x=$\frac{π}{3}$时，求$\overrightarrow m•\overrightarrow n$的值；
（2）若$x∈[{0，\frac{π}{4}}]$，且$\overrightarrow m•\overrightarrow n=\frac{{\sqrt{3}}}{3}-\frac{1}{2}$，求cos2x的值．
1．在平面直角坐标系xoy中，以O为极点，x轴的正半轴为极轴，取相同的单位长度，建立极坐标系．已知曲线C1的参数方程为$\left\{\begin{array}{l}x=\sqrt{3}+2cosα\\ y=3+2sinα\end{array}$，（α∈[0，2π]，α为参数），曲线C2的极坐标方程为$ρsin（{θ+\frac{π}{3}}）=a（{a∈R}）$，若曲线C1与曲线C2有且仅有一个公共点，求实数a的值．
18．若a=sin3，b=sin1.5，c=cos8.5，执行如图所示的程序框图，输出的是（　　）
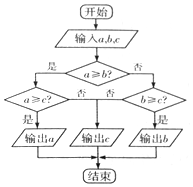
A．cB．bC．aD．$\frac{a+b+c}{3}$
19．从集合{2，3，4，5}中随机抽取一个数a，从集合{4，6，8}中随机抽取一个数b，则向量$\overrightarrow{m}$=（a，b）与向量$\overrightarrow{n}$=（-2，1）垂直的概率为（　　）
A．$\frac{1}{6}$B．$\frac{1}{4}$C．$\frac{1}{3}$D．$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网