题目内容
当a∈[-1,1]时,f(x)=alg2x+4>0恒成立,求x的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:令g(a)=alg2x+4,当lgx≠0时,利用一次函数的性质,解不等式组
即可求得x的取值范围.
|
解答:
解:令g(a)=alg2x+4,
∵a∈[-1,1]时,g(a)=alg2x+4>0恒成立,
∴当a=0时,g(a)=4>0恒成立;
当a≠0且lgx=0,即x=1时,g(a)=4>0恒成立;
当a≠0且lgx≠0时,g(a)=alg2x+4为一次函数,
∴
,即
,
解①有:-2<lgx<2,解得
<x<100且x≠1;
解②得:x∈R,且x≠0.
综上所述,x的取值范围为(
,100).
∵a∈[-1,1]时,g(a)=alg2x+4>0恒成立,
∴当a=0时,g(a)=4>0恒成立;
当a≠0且lgx=0,即x=1时,g(a)=4>0恒成立;
当a≠0且lgx≠0时,g(a)=alg2x+4为一次函数,
∴
|
|
解①有:-2<lgx<2,解得
| 1 |
| 100 |
解②得:x∈R,且x≠0.
综上所述,x的取值范围为(
| 1 |
| 100 |
点评:本题考查函数恒成立问题.考查等价转化思想、函数思想与分类讨论思想的综合应用,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
已知抛物线y2=2px(p>0)的准线与圆x2+y2-4x-5=0相切,则p的值为( )
| A、10 | B、6 | C、4 | D、2 |
已知函数f(x)=2lnx+1的图象与直线y=2x-a恰好有一个交点,设g(x)=ex-x2+a,当x∈[1,2]时,不等式-m≤g(x)≤m2-4恒成立,则实数m的取值范围是( )
A、(-∞,
| ||
B、[
| ||
C、[-e,
| ||
D、[
|
已知
=(2,y,2),
=(x,-1,1),若
⊥
,则实数x,y满足的关系式为( )
| a |
| b |
| a |
| b |
| A、2x-y=0 |
| B、2x+y=0 |
| C、2x+y-2=0 |
| D、2x-y+2=0 |
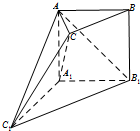 如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.
如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.