题目内容
 随着经济的发展,到某岛进行旅游观光的人数越来越多,交通问题已成为制约经济发展的重要因素,因此政府欲在大陆和岛屿之间(如图)建立一条高速通道以便于大陆和岛屿之间来往,大陆沿海线可近似看作函数f(x)=ax(a>1)的图象,且正好与直线y=x相切,而岛屿海岸线可近似看作函数g(x)=loga(x-3)(a>1)的图象.(每单位代表十万米)
随着经济的发展,到某岛进行旅游观光的人数越来越多,交通问题已成为制约经济发展的重要因素,因此政府欲在大陆和岛屿之间(如图)建立一条高速通道以便于大陆和岛屿之间来往,大陆沿海线可近似看作函数f(x)=ax(a>1)的图象,且正好与直线y=x相切,而岛屿海岸线可近似看作函数g(x)=loga(x-3)(a>1)的图象.(每单位代表十万米)(1)试求a的值及切点坐标.
(2)已知建成后的高速通道将开通高铁,并且高铁的最高时速不能超过300km/h,试问高铁能否在半小时内穿过高速通道?请说明理由.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由题意可设切点为(x0,x0),求出函数的导数,求出切点的斜率,得到切点的横坐标,求出纵坐标,得到结果.
(2)由(1)及f(x)=ax与函数y=logax互为反函数,且f(x)与y=x相切,知f(x)=ax与y=logax相切,此时两曲线只有一个公共点.转化f(x)与g(x)函数图象之间的最短距离S大于直线y=x与直线y=x-3之间的距离,然后求解高铁穿过高速通道时间最小值.
(2)由(1)及f(x)=ax与函数y=logax互为反函数,且f(x)与y=x相切,知f(x)=ax与y=logax相切,此时两曲线只有一个公共点.转化f(x)与g(x)函数图象之间的最短距离S大于直线y=x与直线y=x-3之间的距离,然后求解高铁穿过高速通道时间最小值.
解答:
解:(1)由题意可设切点为(x0,x0),
则f′(x0)=ax0ln a=1,
得ax0=
,
x0=loga(
)=-loga(lna)=
,
又因为ax0=x0,所以
=
,解得a=e
,x0=e,
即切点坐标为(e,e).5分
(2)由(1)及f(x)=ax与函数y=logax互为反函数,
且f(x)与y=x相切,知f(x)=ax与y=logax相切,
此时两曲线只有一个公共点.
而g(x)=loga(x-3)可由y=logax向右平移3个单位而得到,
所以f(x)与g(x)函数图象之间的最短距离S大于直线y=x与直线y=x-3之间的距离,
即S>
=
(十万米)=
(km).
所以高铁穿过通道的时间t>
=
>
.
故高铁不能在半小时内穿过高速通道.12分.
则f′(x0)=ax0ln a=1,
得ax0=
| 1 |
| lna |
x0=loga(
| 1 |
| lna |
| -ln(lna) |
| lna |
又因为ax0=x0,所以
| 1 |
| lna |
| -ln(lna) |
| lna |
| 1 |
| e |
即切点坐标为(e,e).5分
(2)由(1)及f(x)=ax与函数y=logax互为反函数,
且f(x)与y=x相切,知f(x)=ax与y=logax相切,
此时两曲线只有一个公共点.
而g(x)=loga(x-3)可由y=logax向右平移3个单位而得到,
所以f(x)与g(x)函数图象之间的最短距离S大于直线y=x与直线y=x-3之间的距离,
即S>
| |3| | ||
|
3
| ||
| 2 |
300
| ||
| 2 |
所以高铁穿过通道的时间t>
| ||||
| 300 |
| ||
| 2 |
| 1 |
| 2 |
故高铁不能在半小时内穿过高速通道.12分.
点评:本题考查函数与导数的应用,函数与反函数的关系,函数与方程的思想,实际问题的分析以及解决问题的方法,考查转化思想的应用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知集合A,B,则“A⊆B”是“A∩B=A”的( )条件.
| A、充分不必要 |
| B、充要 |
| C、必要不充分 |
| D、既非充分又非必要 |
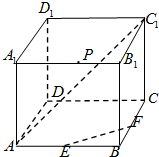 在长方体ABCD-A1B1C1D1中,AB=AA1=4,BC=3,E、F分别是所在棱AB、BC的中点,点P是棱A1B1上的动点,联结EF,AC1.如图所示.
在长方体ABCD-A1B1C1D1中,AB=AA1=4,BC=3,E、F分别是所在棱AB、BC的中点,点P是棱A1B1上的动点,联结EF,AC1.如图所示.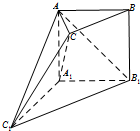 如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.
如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.