题目内容
20.若ab=-2,则a2+b2-1的最小值为3.分析 利用重要不等式的性质即可得出.
解答 解:∵ab=-2,则a2+b2-1≥-2ab-1=4-1=3,当且仅当a=-b=-$\sqrt{2}$时取等号.
因此最小值为3.
故答案为:3.
点评 本题考查了重要不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.给出如下四个命题:①e${\;}^{\frac{2}{e}}$>2②ln2>$\frac{2}{3}$③π2<3π④$\frac{ln2}{2}$<$\frac{lnπ}{π}$,正确的命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.已知曲线C1:y2=tx (y>0,t>0)在点M($\frac{4}{t}$,2)处的切线与曲线C2:y=ex+l-1也相切,则t的值为( )
| A. | 4e2 | B. | 4e | C. | $\frac{e^x}{4}$ | D. | $\frac{e}{4}$ |
15.若${(a+i)^2}-\frac{1}{i}∈R(a∈R,i$是虚数单位),则a=( )
| A. | 1 | B. | 0 | C. | 一$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
2.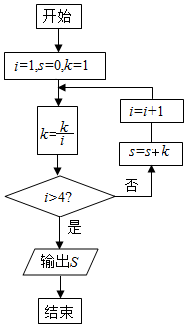 阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
 阅读如图的程序框图,运行相应的程序,则输出的S的值为( )
阅读如图的程序框图,运行相应的程序,则输出的S的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{41}{24}$ | D. | $\frac{103}{60}$ |
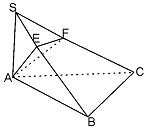 如图所示,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.
如图所示,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.