题目内容
11.函数f(x)的导函数f′(x)在R上恒大于0,则对任意x1,x2(x1≠x2)在R上$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$的符号是正(填“正”、“负”)分析 根据函数的导数的符号,判断函数的单调性,以及函数的割线的斜率进行求解即可.
解答 解:∵函数f(x)的导函数f′(x)在R上恒大于0,
∴函数f(x)为增函数,
即函数f(x)在定义域上的割线斜率k=$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,
故答案为:正
点评 本题主要考查函数单调性和导数的关系,根据函数导数的符号和单调性的关系是解决本题的关键.

练习册系列答案
相关题目
2.已知等比数列{an}的前n项和为Sn,且S2+a2,S1+2a2,S3+a3,成等差数列,则数列{an}的公比为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
6.函数g(x)=-x2+2lnx的图象大致是( )
| A. |  | B. | 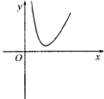 | C. | 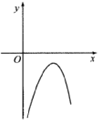 | D. | 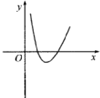 |
16.设集合M=$\left\{{\left.x\right|x=tan\frac{π}{4}}\right\}$,N=$\left\{{\frac{1}{2},\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2},\sqrt{3}}\right\}$,则M∩N=( )
| A. | M | B. | $\left\{{\frac{{\sqrt{2}}}{2}}\right\}$ | C. | ∅ | D. | {0} |
 如图所示的伪代码:
如图所示的伪代码: