题目内容
1.设ω为正实数,若存在a,b(π≤a<b≤2π),使得cosωa+cosωb=2,则ω的取值范围是{2}∪[3,+∞).分析 运用三角函数的有界性,结合三角函数的周期性,分析得到答案.
解答 解:要cosωa+cosωb=2,则有cosωa=cosωb=1;
余弦函数y=cosx图象如下: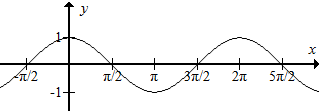
可知,当x=2kπ时,cosx=1,
∵cosωa+cosωb=2,π≤a<b≤2π
∴必有ωa=2kπ,ωb=2kπ+nπ,(k,n∈N+),
∴$\left\{\begin{array}{l}{ωπ≤2kπ}\\{ω•2π≥2kπ+2π}\end{array}\right.,k∈{N}_{+}$
得到k+1≤ω≤2k(k∈N+),
①k=1时,ω=2,
②k=2时,3≤ω≤4,
③k=3时,4≤ω≤6,
④k=4时,5≤ω≤8,
…
可得ω的取值范围为{2}∪[3,+∞).
点评 本题考查三角函数的值域,涉及不等式的性质和分类讨论的思想,属中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
11.设函数f(x)=$\sqrt{3}$sin(ωx+φ)+cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为2π,且其图象关于y轴对称,则( )
| A. | f(x)在(0,$\frac{π}{2}$)上单调递增 | B. | f(x)在($\frac{π}{4}$,$\frac{3π}{2}$)上单调递减 | ||
| C. | f(x)在(0,$\frac{π}{2}$)上单调递减 | D. | f(x)在($\frac{π}{4}$,$\frac{3π}{2}$)上单调递增 |