题目内容
在锐角△ABC中，角A，B，C所对的边分别为a，b，c，且asinB=
bcosA．
（1）求A的大小；
（2）若a=3，sinC=2sinB，求b，c的值．
| 3 |
（1）求A的大小；
（2）若a=3，sinC=2sinB，求b，c的值．
考点：余弦定理的应用,正弦定理的应用
专题：解三角形
分析：（1）利用正弦定理结合已知条件即可求解A的三角函数值，然后求解A的大小；
（2）通过a=3，利用正弦定理化简sinC=2sinB，然后利用余弦定理，即可求b，c的值．
（2）通过a=3，利用正弦定理化简sinC=2sinB，然后利用余弦定理，即可求b，c的值．
解答：
（本小题满分14分）
解：（1）由正弦定理得 sinAsinB=
sinBcosA
∵B∈（0，π），∴sinB≠0
∴sinA=
cosA，∴tanA=
又∵A∈（0，π），∴A=
…（7分）
（2）∵sinC=2sinB，由正弦定理，得c=2b
由余弦定理，得cosA=
，
将A=
，a=3，c=2b代入，得
=
，
∴b=
，c=2
．…（14分）
解：（1）由正弦定理得 sinAsinB=
| 3 |
∵B∈（0，π），∴sinB≠0
∴sinA=
| 3 |
| 3 |
又∵A∈（0，π），∴A=
| π |
| 3 |
（2）∵sinC=2sinB，由正弦定理，得c=2b
由余弦定理，得cosA=
| b2+c2-a2 |
| 2bc |
将A=
| π |
| 3 |
| 1 |
| 2 |
| b2+4b2-9 |
| 2b•2b |
∴b=
| 3 |
| 3 |
点评：本题考查正弦定理以及余弦定理的应用，考查基本知识的应用．
练习册系列答案
名校课堂系列答案
相关题目
已知圆C的方程是x2+y2-8x-2y+10=0，过点M（3，0）的最短弦所在的直线方程是（ ）
| A、x+y-3=0 |
| B、x-y-3=0 |
| C、2x-y-6=0 |
| D、2x+y-6=0 |
已知：p：x＜k，q：x≤1，如果p是q的充分不必要条件，则k的取值范围是（ ）
| A、[2，+∞） |
| B、（2，+∞） |
| C、（-∞，-1） |
| D、（-∞，1] |
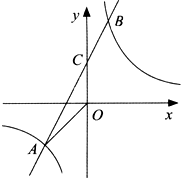如图，已知A（n，-2），B（1，4）是一次函数y=kx+b的图象和反比例函数y=
