题目内容

1．多项式$（{4{x^2}-2}）{（{1+\frac{1}{x^2}}）^5}$展开式中的常数项是18．

分析 多项式$（{4{x^2}-2}）{（{1+\frac{1}{x^2}}）^5}$=（4x2-2）$（1+\frac{5}{{x}^{2}}+…）$，即可得出其展开式中的常数项．

解答 解：多项式$（{4{x^2}-2}）{（{1+\frac{1}{x^2}}）^5}$=（4x2-2）$（1+\frac{5}{{x}^{2}}+…）$，
其展开式中的常数项为：-2+4×5=18．
故答案为：18．

点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
11．已知抛物线 Γ：y2=8x 的焦点为 F，准线与 x 轴的交点为K，点 P 在 Γ 上且$|{PK}|=\sqrt{2}|{PF}|$，则△PKF的面积为8．
12．已知α是第一象限角，满足$sinα-cosα=\frac{{\sqrt{10}}}{5}$，则cos2α=（　　）
A．-$\frac{3}{5}$B．$±\frac{3}{5}$C．$-\frac{4}{5}$D．$±\frac{4}{5}$
9．据统计，用于数学学习的时间（单位：小时）与成绩（单位：分）近似于线性相关关系．对某小组学生每周用于数学学习时间x与数学成绩y进行数据收集如表：
x1516181922
y10298115115120
由表中样本数据求回归直线方程$\stackrel{∧}{y}$=bx+a，则点（a，b）与直线x+18y=110的位置关系为是（　　）
A．点在直线左侧B．.点在直线右侧C．.点在直线上D．无法确定
16．中国传统文化中不少优美的古诗词很讲究对仗，如“明月松间照，清泉石上流”中明月对清泉同为自然景物，明和清都是形容词，月和泉又都是名词，数学除了具有简洁美、和谐美、奇异美外，也具有和古诗词中对仗类似的对称美．请你判断下面四个选项中，体现数学对称美的是（　　）
A．“$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{100}$”表示成“$\sum_{k=1}^{100}{\frac{1}{k}}$”
B．平面上所有二次曲线的一般形式均可表示成：Ax2+Bxy+Cy2+Dx+Ey+F=0
C．正弦定理：$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$
D．123456789×9+10=1111111111
6．设集合A={x|x-3＜0}，B={y|y=2x，x∈[1，2]}，则A∩B=（　　）
A．∅B．（1，3）C．[2，3）D．（1，4]
13．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x}-1，（x＜1）}\\{{x}^{3}-9{x}^{2}+24x-16，（x≥1）}\end{array}\right.$，则关于x的方程f（x）=a（a为实数）根个数不可能为（　　）
A．2B．3C．4D．5
10．下方茎叶图如图1，为高三某班50名学生的数学考试成绩，算法框图如图2中输入的ai为茎叶图中的学生成绩，则输出的m，n分别是（　　）
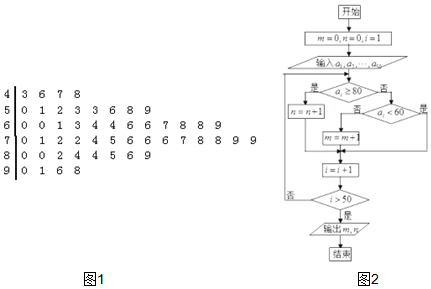
A．m=26，n=12B．m=38，n=12C．m=12，n=12D．m=24，n=10
11．已知函数$f（x）=\left\{\begin{array}{l}{log_{\frac{1}{3}}}x，x＞0\\{2^x}，x≤0\end{array}\right.$，若$f（a）＞\frac{1}{2}$，则实数a的取值范围是（　　）
A．$（{0，\frac{{\sqrt{3}}}{3}}）$B．（-1，0]C．$（{-1，\frac{{\sqrt{3}}}{3}}）$D．$（{-1，0}）∪（{0，\frac{{\sqrt{3}}}{3}}）$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网