题目内容
11.已知抛物线 Γ:y2=8x 的焦点为 F,准线与 x 轴的交点为K,点 P 在 Γ 上且$|{PK}|=\sqrt{2}|{PF}|$,则△PKF的面积为8.分析 设P(x,y),K(-2,0),F(2,0),由$|{PK}|=\sqrt{2}|{PF}|$,及点P在抛物线上,利用两点间的距离公式可得关于x,y的方程,解方程可求P的坐标,进而可求△PFK的面积.
解答 解:由题意,设P(x,y),K(-2,0),F(2,0),
∵$|{PK}|=\sqrt{2}|{PF}|$,
∴$\sqrt{(x+2)^{2}+{y}^{2}}$=$\sqrt{2}•\sqrt{(x-2)^{2}+{y}^{2}}$,
整理可得,x2+y2-12x+4=0,
∵y2=8x,
∴x2-4x+4=0,
∴x=2,|y|=4,
∴S△PFK=$\frac{1}{2}$|FK||y|=$\frac{1}{2}×4×4$=8.
故答案为:8
点评 本题主要考查了抛物线的性质的简单应用及基本的运算能力,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}sin({x+α}),({x≤0})\\ cos({x-β}),({x>0})\end{array}$是偶函数,则下列结论可能成立的是( )
| A. | $α=\frac{π}{4},β=\frac{π}{8}$ | B. | $α=\frac{2π}{3},β=\frac{π}{6}$ | C. | $α=\frac{π}{3},β=\frac{π}{6}$ | D. | $α=\frac{5π}{6},β=\frac{2π}{3}$ |
6.小赵、小钱、小孙、小李到 4 个景点旅游,每人只去一个景点,设事件 A=“4 个人去的景点不相同”,事件B=“小赵独自去一个景点”,则P( A|B)=( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
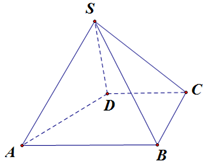 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.