题目内容
已知椭圆C:
+
=1(a>b>0)的离心率e=
,以坐标原点O为圆心,半径为c(c为椭圆的半焦距)的圆O与直线l:y=-
x+3相切.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l与圆O的公共点为M,与椭圆C的公共点为N,求△OMN的面积.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l与圆O的公共点为M,与椭圆C的公共点为N,求△OMN的面积.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)可设圆O的方程为x2+y2=c2,根据圆O到直线的距离等于半径c可求c值,由离心率可得a,再由b2=a2-c2可求得方程;
(Ⅱ)由
得9x2-24
x+32=0,解出可得N点坐标,从而可得|ON|、|OM|,由沟谷定理可得|MN|,利用三角形面积公式可求△OMN的面积.
(Ⅱ)由
|
| 2 |
解答:
解:(Ⅰ)根据题意,圆O的方程为x2+y2=c2,
于是可得圆心O(0,0)到直线l:y=-
x+3的距离为c,即有
=c,c=
,
又∵e=
=
,∴a=2,
∴b2=a2-c2=1,
∴椭圆的方程为
+y2=1.
(Ⅱ)由
得9x2-24
x+32=0,
设N(x1,y1),
则x1=
,y1=
,由直线与椭圆相切,知M为切点,
∴|ON|=
=
,
又|OM|=
,
∴|MN|=
=
=
,
∴S△OMN=
•|MN||OM|=
×
×
=
.
于是可得圆心O(0,0)到直线l:y=-
| 2 |
| 3 | ||
|
| 3 |
又∵e=
| c |
| a |
| ||
| 2 |
∴b2=a2-c2=1,
∴椭圆的方程为
| x2 |
| 4 |
(Ⅱ)由
|
| 2 |
设N(x1,y1),
则x1=
4
| ||
| 3 |
| 1 |
| 3 |
∴|ON|=
| x12+y12 |
| ||
| 3 |
又|OM|=
| 3 |
∴|MN|=
| |ON|2-|OM|2 |
|
| ||
| 3 |
∴S△OMN=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 3 |
| ||
| 2 |
点评:本题考查椭圆的方程性质、直线与圆锥曲线的位置关系、三角形面积公式,考查方程思想、数形结合思想,考查学生运算求解能力,准确运算是解决该类题目的基础.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
定义在R上的函数f(x)满足f(x+2)=f(x),当x∈[1,3],f(x)=2-|x-2|,则下列结论中正确的是( )
A、f(sin
| ||||
| B、f(sin1)>f(cos1) | ||||
C、f(cos
| ||||
| D、f(cos2)>f(sin2) |
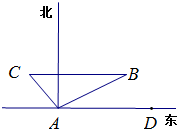 如图,海警观察站设在海岸A处,某天值班海警发现北偏东60°方向,距离A处10
如图,海警观察站设在海岸A处,某天值班海警发现北偏东60°方向,距离A处10 如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=x(x≥0)重合,点B的纵坐标为
如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=x(x≥0)重合,点B的纵坐标为