题目内容
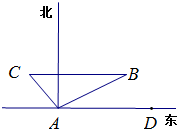 如图,海警观察站设在海岸A处,某天值班海警发现北偏东60°方向,距离A处10
如图,海警观察站设在海岸A处,某天值班海警发现北偏东60°方向,距离A处10| 3 |
| 3 |
(Ⅰ)两缉私船在接到命令时,相距多少海里;
(Ⅱ)若一号缉私船和二号缉私船恰好能以最短的时间同时追上走私船,求最短时间和二号缉私船的速度v.
考点:解三角形的实际应用
专题:应用题,解三角形
分析:(Ⅰ)由题意,AC=10海里,AD=20海里,∠CAD=120°,利用余弦定理,可得结论;
(Ⅱ)先求出BC,再利用余弦定理计算最短时间和二号缉私船的速度v.
(Ⅱ)先求出BC,再利用余弦定理计算最短时间和二号缉私船的速度v.
解答:
解:(Ⅰ)由题意,AC=10海里,AD=20海里,∠CAD=120°,
∴CD=
=10
海里;
(Ⅱ)∵AC=10海里,AB=10
海里,∠CAB=90°,
∴BC=20,
设在E处追上,最短时间为t,则CE=10
t,BE=10t,∠CBE=120°,
∴(10
t)2=400+(10t)2-2•20•10t•cos120°,
∴t2-t-2=0,
∴t=2,
∵BC=AD,BC∥AD,
∴BD=AC=10海里,
在△BDE中,BD=10海里,BE=20,∠BDE=120°,DE=2v,则
(2v)2=102+202-2•10•20•cos120°,
∴v=15海里每小时.
∴CD=
100+400-2×10×20×(-
|
| 7 |
(Ⅱ)∵AC=10海里,AB=10
| 3 |
∴BC=20,
设在E处追上,最短时间为t,则CE=10
| 3 |
∴(10
| 3 |
∴t2-t-2=0,
∴t=2,
∵BC=AD,BC∥AD,
∴BD=AC=10海里,
在△BDE中,BD=10海里,BE=20,∠BDE=120°,DE=2v,则
(2v)2=102+202-2•10•20•cos120°,
∴v=15海里每小时.
点评:本题考查利用数学知识解决实际问题,考查余弦定理的运用,正确计算是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知M={y|y=x2},N={x|
+y2=1},则M∩N=( )
| x2 |
| 2 |
| A、{(-1,1),(1,1)} | ||
| B、{1} | ||
C、[0,
| ||
| D、[0,1] |