Question

已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-

π

2

＜φ＜

π

2

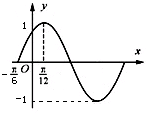
）的图象与x轴交点为(-

π

6

，0)，相邻最高点坐标为(

π

12

，1)．
（1）求函数f（x）的表达式；
（2）求函数g(x)=log

1

2

f（x）的单调增区间．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,复合函数的单调性

专题：三角函数的图像与性质

分析：（1）根据已知依次确定A，ω，φ的值，即可求函数f（x）的表达式；
（2）由复合函数的单调性及定义域可求g(x)=log

1

2

f(x)的单调增区间．

解答： 解：（1）从图知，函数的最大值为1，
则A=1  函数f（x）的周期为T=4×(

π

12

+

π

6

)=π，而T=

2π

ω

，则ω=2，
又x=-

π

6

时，y=0，
∴sin[2×(-

π

6

)+φ]=0，而-

π

2

＜φ＜

π

2

，则φ=

π

3

，
∴函数f（x）的表达式为f（x）=sin（2x+

π

3

）；

（3）由复合函数的单调性及定义域可求g(x)=log

1

2

f(x)的单调增区间：由2kπ+

π

2

＜2x+

π

3

＜2kπ+π得kπ+

π

12

＜x＜kπ+

π

3

，k∈Z，
所以g(x)=log

1

2

f(x)的单调增区间为(kπ+

π

12

，kπ+

π

3

)，k∈Z．

点评：本题主要考察了由y=Asin（ωx+φ）的部分图象确定其解析式，复合函数的单调性的求法，属于中档题．