题目内容
下列说法中不正确的个数是（ ）
①y=sinx的递增区间是[2kπ，2kπ+
]（k∈Z）；
②y=sinx在第一象限是增函数；
③y=cosx在[-π，0]上是增函数；
④y=tanx在其定义域上是增函数．
①y=sinx的递增区间是[2kπ，2kπ+
| π |
| 2 |
②y=sinx在第一象限是增函数；
③y=cosx在[-π，0]上是增函数；
④y=tanx在其定义域上是增函数．
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：命题的真假判断与应用
专题：三角函数的图像与性质
分析：由正弦函数y=sinx单调性可判断①的正误；
与
均为第一象限的角，且
＜
，但sin
＞sin
，可判断②的正误；
利用余弦函数y=cosx的单调性质可判断③的正误；
举例说明，
＜
，但tan
=1＞-1=tan
，可判断④的正误．
| π |
| 3 |
| 13π |
| 6 |
| π |
| 3 |
| 13π |
| 6 |
| π |
| 3 |
| 13π |
| 6 |
利用余弦函数y=cosx的单调性质可判断③的正误；
举例说明，
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
解答：
解：对于①，y=sinx的递增区间是[2kπ-
，2kπ+
]（k∈Z），故①错误；
对于②，y=sinx在每一个区间（2kπ，2kπ+
）（k∈Z）是增函数，并不是第一象限是增函数，如
与
均为第一象限的角，且
＜
，但sin
＞sin
，故②错误；
对于③，由余弦函数的单调性可知，y=cosx在[-π，0]上是增函数，故③正确；
对于④，y=tanx在（kπ-
，kπ+
）（k∈Z）上单调递增，并不是在定义域上是增函数，如
＜
，但tan
=1＞-1=tan
，故④错误．
综上所述，以上说法中不正确的个数是3个，
故选：C．
| π |
| 2 |
| π |
| 2 |
对于②，y=sinx在每一个区间（2kπ，2kπ+
| π |
| 2 |
| π |
| 3 |
| 13π |
| 6 |
| π |
| 3 |
| 13π |
| 6 |
| π |
| 3 |
| 13π |
| 6 |
对于③，由余弦函数的单调性可知，y=cosx在[-π，0]上是增函数，故③正确；
对于④，y=tanx在（kπ-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
综上所述，以上说法中不正确的个数是3个，
故选：C．
点评：本题考查命题的真假判断与应用，着重考查正弦函数、余弦函数及正切函数的单调性，属于中档题．
练习册系列答案
相关题目
已知点A（1，2），B（3，1），则线段AB的垂直平分线的方程为（ ）
| A、4x+2y-5=0 |
| B、4x-2y-5=0 |
| C、x+2y-5=0 |
| D、x-2y-5=0 |
复数1-i在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
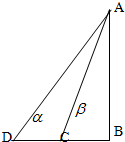如图：D，C，B三点在地面同一直线上，DC=a，从C，D两点测得A点仰角分别是β，α（α＜β），则A点离地面的高度AB等于
