题目内容
15.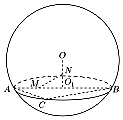 如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3,O1为截面小圆圆心,AB为截面小圆的直径;
如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3,O1为截面小圆圆心,AB为截面小圆的直径;(1)计算球O的表面积和体积;
(2)若C是截面小圆上一点,∠ABC=30°,M、N分别是线段AO1和OO1的中点,求
异面直线AC与MN所成的角;(结果用反三角表示)
分析 (1)求出小圆的半径,然后利用球心到该截面的距离为3cm,小圆的半径,通过勾股定理求出球的半径,即可求出球的表面积.
(2)由MN∥OA得,∠OAC为异面直线AC与MN所成的角(或补角),连接OC,然后利用余弦定理求出此角的余弦值,最后利用反三角表示出此角即可.
解答 解:(1)连接OA,由题意得,截面小圆半径为4,(2分)
在Rt△OAO1中,O1A=4,OO1=3,
由勾股定理知,AO=5,(4分)
∴球O的表面积为:4π•25=100π(7分)
(2)由MN∥OA得,∠OAC为异面直线AC与MN所成的角(或补角).(9分)
在Rt△ABC中,AB=8,∠ABC=30°,则AC=4,(10分)
连接OC,在△OAC中,OA=OC=5,
由余弦定理知:
cos∠OAC=$\frac{A{C}^{2}+O{A}^{2}-O{C}^{2}}{2OA•AC}$=$\frac{{4}^{2}+{5}^{2}-{5}^{2}}{2×4×5}$=$\frac{2}{5}$,
∴∠OAC=$arccos\frac{2}{5}$,
∴异面直线AC与MN所成的角为$arccos\frac{2}{5}$.
点评 本题主要考查了球的表面积,以及异面直线及其所成角和余弦定理的应用,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.下列说法正确的是( )
| A. | 任何事件的概率总是在(0,1)之间 | |
| B. | 频率是客观存在的,与试验次数无关 | |
| C. | 概率是随机的,在试验前不能确定 | |
| D. | 随着试验次数的增加,频率一般会越来越接近概率 |
5.圆(x-2)2+(y+3)2=1的圆心坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (-2,-3) | D. | (2,-3) |
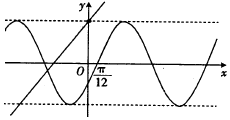 已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.
已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.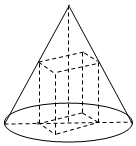 底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).