题目内容
6.已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上动点P,Q,O为原点:(1)若|OP|2+|OQ|2=a2+b2,求证:|kOP•kOQ|为定值;
(2)点B(0,b),若BP⊥BQ,求证:直线PQ过定点;
(3)若OP⊥OQ,求证:直线PQ为定圆的切线.
分析 (1)由题意可知|OP|2+|OQ|2=x12+y12+x22+y22=a2+b2,将P,Q代入椭圆方程,求得x12+x22=a2,利用直线的斜率公式,即可求证|kOP•kOQ|为定值;
(2)将直线方程代入椭圆方程,利用韦达定理及直线的斜率公式,即可求得m的值,则直线PQ过定点;
(3)设y=kx(k≠0),则OQ方程为:y=$\frac{1}{k}$x,分别代入椭圆方程,利用韦达定理及三角形的性质,O到直线PQ的距离d为定值,即可求得直线PQ为定圆x2+y2=$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$的切线.
解答 证明:(1)由题意可知:设P(x1,y1),Q(x2,y2),|OP|2+|OQ|2=x12+y12+x22+y22=a2+b2,
由P,Q在椭圆上,则y12=b2(1-$\frac{{x}_{1}^{2}}{{a}^{2}}$),y22=b2(1-$\frac{{x}_{2}^{2}}{{a}^{2}}$),代入整理得:x12+x22=a2,
则|kOP•kOQ|=$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{2}}{{x}_{2}}$=$\sqrt{\frac{{y}_{1}^{2}•{y}_{2}^{2}}{{x}_{1}^{2}•{x}_{1}^{2}}}$=$\sqrt{\frac{{b}^{2}(1-\frac{{x}_{1}^{2}}{{a}^{2}})•{b}^{2}(1-\frac{{x}_{2}^{2}}{{a}^{2}})}{{x}_{1}^{2}•{x}_{2}^{2}}}$=b2$\sqrt{\frac{1-\frac{1}{{a}^{2}}({x}_{1}^{2}+{x}_{2}^{2})+\frac{1}{{a}^{4}}{x}_{1}^{2}{x}_{2}^{2}}{{x}_{1}^{2}{x}_{2}^{2}}}$=$\frac{{b}^{2}}{{a}^{2}}$,
∴|kOP•kOQ|为定值$\frac{{b}^{2}}{{a}^{2}}$;
(2)易知,直线PQ的斜率存在,设其方程为y=kx+m,设 P(x1,y1),Q(x2,y2),
$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,消去y,整理得 (b2+a2k2)x2+2a2kmx+a2m2-a2b2=0.
则 x1+x1=-$\frac{2{a}^{2}km}{{b}^{2}+{a}^{2}{k}^{2}}$,x1x2=$\frac{{a}^{2}{m}^{2}-{a}^{2}{b}^{2}}{{b}^{2}+{a}^{2}{k}^{2}}$,
由BP⊥BQ,且直线BP,BQ的斜率均存在,
∴$\frac{{y}_{1}-b}{{x}_{1}}$•$\frac{{y}_{2}-b}{{x}_{1}}$=-1,整理得 x1x2+y1y2-b2(y1+y2)+b2=0.
因为 y1=kx1+m,y2=kx2+m,
所以 y1+y2=k(x1+x2)+2m,y1y1=k2x1x2+km(x1+x1)+m2.
整理得(1+k2)x1x2+k(m-b2)(x1+x1)+m2-2b2m+b2=0.
∴(a2+b2)m2-2b3m-b2(a2-b2)=0.(13分)
解得 m=-$\frac{b({a}^{2}-{b}^{2})}{{a}^{2}+{b}^{2}}$,或m=b(舍去).
∴直线PQ恒过定点(0,-$\frac{b({a}^{2}-{b}^{2})}{{a}^{2}+{b}^{2}}$),
(3)设OP方程为:y=kx(k≠0),P(x1,y1),Q(x2,y2),
则OQ方程为:y=$\frac{1}{k}$x,
联立$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,可得:x12=$\frac{{a}^{2}+{b}^{2}}{{k}^{2}{a}^{2}+{b}^{2}}$,
∴丨OP丨2=(1+k2)x12=$\frac{{a}^{2}{b}^{2}(1+{k}^{2})}{{a}^{2}{k}^{2}+{b}^{2}}$,
同理可得:丨OQ丨2=$\frac{{a}^{2}{b}^{2}(1+{k}^{-2})}{{k}^{-2}{a}^{2}+{b}^{2}}$=$\frac{{a}^{2}{b}^{2}(1+{k}^{2})}{{k}^{2}{b}^{2}+{a}^{2}}$
则O到直线PQ的距离d,即为△POQ斜边上的高,
d=$\frac{丨OP丨•丨OR丨}{丨PQ丨}$=$\sqrt{\frac{丨OP{丨}^{2}•丨OQ{丨}^{2}}{丨PQ{丨}^{2}}}$=$\sqrt{\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}}$,(定值).
则直线PQ为定圆x2+y2=$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$的切线.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于中档题.

| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
| A. | (-∞,-2] | B. | (-2,+∞) | C. | (-2,-$\frac{1}{8}$) | D. | $[-\frac{1}{8},+∞)$ |
| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $±2\sqrt{2}$ | D. | $±4\sqrt{2}$ |
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{10}$ |




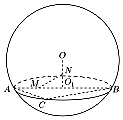 如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3,O1为截面小圆圆心,AB为截面小圆的直径;
如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3,O1为截面小圆圆心,AB为截面小圆的直径;