题目内容
4.已知正项数列{an}满足an+12-2an2=anan+1,若a1=1,则数列{an}的前n项和为Sn=2n-1.分析 把已知的数列递推式变形,因式分解后得到数列{an}是公比为2的等比数列,然后由等比数列的前n项和公式得答案.
解答 解:∵an+12-2an2=anan+1,
∴an+12-anan+1-2an2=0,即(an+1+an)(2an-an+1)=0,
又an>0,∴2an-an+1=0,即$\frac{{a}_{n+1}}{{a}_{n}}=2$,
∴数列{an}是公比为2的等比数列,
又∵a1=2,
∴数列{an}的前n项和为Sn=$\frac{1×(1-{2}^{n})}{1-2}={2}^{n}-1$.
故答案为:2n-1.
点评 本题考查了数列递推式,考查了等比关系的确定,训练了等比数列前n项和的求法,是中档题.

练习册系列答案
相关题目
19.已知某几何体的三视图如图所示,则该几何体的体积为( )
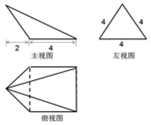

| A. | $\frac{32}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{{32\sqrt{3}}}{3}$ | D. | $\frac{{64\sqrt{3}}}{3}$ |
16.若tanα=$\frac{1}{3}$,则sin4α-cos4α+6sin$\frac{α}{2}$cos$\frac{α}{2}$cosα=( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{10}$ |
13.已知方程$\frac{{x}^{2}}{2+m}$-$\frac{{y}^{2}}{m+1}$=1表示双曲线,则实数m的取值范围是( )
| A. | (-1,∞) | B. | (-2,-1) | C. | (-∞,-2)∪(-1,+∞) | D. | (-∞,-2) |
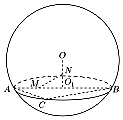 如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3,O1为截面小圆圆心,AB为截面小圆的直径;
如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3,O1为截面小圆圆心,AB为截面小圆的直径; 如图,将正三角形ABC分割成m个边长为1的小正三角形和一个灰色菱形,这个灰色菱形可以分割成n个边长为1的小正三角形.若m:n=47:25,则三角形ABC的边长是( )
如图,将正三角形ABC分割成m个边长为1的小正三角形和一个灰色菱形,这个灰色菱形可以分割成n个边长为1的小正三角形.若m:n=47:25,则三角形ABC的边长是( )