Question

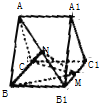如图，在直三棱柱ABC-A₁B₁C₁中，AA₁=AC=1，BC=

2

，AB=

3

，M是棱B₁C₁的中点，N是对角线AB₁的中点．
（1）求证：CN⊥平面BNM；
（2）求三棱锥M-BCN的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面垂直的判定

专题：空间位置关系与距离,空间向量及应用

分析：（1）运用坐标系

CN

=（

2

2

，

1

2

，

1

2

），

BM

=（-

2

2

，1，0），

BN

=（-

2

2

，

1

2

，

1

2

），得出

CN

•

BM

=0，

CN

•

BN

=0，可证垂直．
（2））运用向量求出|

CN

|=1，|

BM

|=

6

2

，|

BN

|=1，cos∠MBN=

1

1× 6 2

=

6

3

，S_△MBN面积，可得出体积．

解答： 证明：（1）
建立坐标系，以CB为x轴，以CC₁为y轴，以CA为z轴，
∵AA₁=AC=1，BC=

2

，AB=

3

，M是棱B₁C₁的中点，N是对角线AB₁的中点．
∴C（0，0，0），A（0，0，1），B₁（

2

，1，0），C（0，1，0），B（

2

，0，0），N（

2

2

，

1

2

，

1

2

），M（

2

2

，1，0），
∴

CN

=（

2

2

，

1

2

，

1

2

），

BM

=（-

2

2

，1，0），

BN

=（-

2

2

，

1

2

，

1

2

），
∴

CN

•

BM

=0，

CN

•

BN

=0，
∴

CN

⊥

BM

，

CN

⊥

BN

，
∵BM∩BN=B
∴CN⊥平面BNM；
（2）|

CN

|=1，|

BM

|=

6

2

，|

BN

|=1，cos∠MBN=

1

1× 6 2

=

6

3

，
∴sin∠MBN=

3

3

S_△MBN=

1

2

×1×

6

2

×

3

3

=

2

4

，
∴三棱锥M-BCN的体积为：

1

3

×

2

4

×1=

2

12

．

点评：本题考查了运用空间向量求解结合体的体积，面积，垂直问题，属于中档题，难度不是很大，但是容易计算出错．