题目内容
设α是第一象限角,且cosα=
,求:
.
| 5 |
| 13 |
| 2sin(α-3π)-3cos(-α) |
| 4sin(α-5π)+9cos(3π+α) |
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:由已知求出sinα,利用诱导公式化简
,代值后得答案.
| 2sin(α-3π)-3cos(-α) |
| 4sin(α-5π)+9cos(3π+α) |
解答:
解:∵α是第一象限角,且cosα=
,
则sinα=
=
=
,
∴
=
=
=
=
=
.
| 5 |
| 13 |
则sinα=
| 1-cos2α |
1-(
|
| 12 |
| 13 |
∴
| 2sin(α-3π)-3cos(-α) |
| 4sin(α-5π)+9cos(3π+α) |
=
| -2sin(3π-α)-3cosα |
| -4sin(5π-α)+9cos(3π+α) |
=
| -2sin(π-α)-3cosα |
| -4sin(π-α)+9cos(π+α) |
=
| -2sinα-3cosα |
| -4sinα-9cosα |
=
-2×
| ||||
-4×
|
=
| 13 |
| 31 |
点评:本题考查了同角三角函数的基本关系式,考查了诱导公式的应用,是基础的计算题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
若异面直线l1,l2的方向向量分别是
=(0,-2,-1),
=(2,0,4),则异面直线l1与l2的夹角的余弦值等于( )
| a |
| b |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
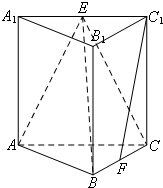 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,A1B1⊥BC,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,A1B1⊥BC,BC=1,AA1=AC=2,E、F分别为A1C1、BC的中点.(Ⅰ)求证:C1F∥平面EAB;
(Ⅱ)求三棱锥A-BCE的体积.
若非零向量
,
,满足|
|=|
|=|
-
|,则
与
-
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
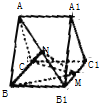 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=