题目内容
已知f(x)=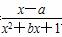 是奇函数.
是奇函数.
(1)求a,b的值;
(2)求f(x)的单调区间,并加以证明;
(3)求f(x)(x>0)的最值.
(1)∵f(x)+f(-x)=0恒成立,
即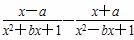 =0恒成立,
=0恒成立,
则2(a+b)x2+2a=0对任意的实数x恒成立.
∴a=b=0.
(2)∵f(x)=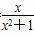 (x∈R)是奇函数,
(x∈R)是奇函数,
∴只需研究(0,+∞)上f(x)的单调区间即可.
任取x1,x2∈(0,+∞),且x1<x2,则
f(x1)-f(x2)=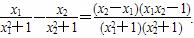 ∵x
∵x +1>0,x
+1>0,x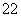 +1>0,x2-x1>0,
+1>0,x2-x1>0,
而x1,x2∈[0,1]时,x1x2-1<0,
∴当x1,x2∈[0,1]时,f(x1)-f(x2)<0,
函数y=f(x)是增加的;
当x1,x2∈[1,+∞)时,f(x1)-f(x2)>0,
函数y=f(x)是减少的.
又f(x)是奇函数,
∴f(x)在[-1,0]上是增加的,在(-∞,-1]上是减少的.
又x∈[0,1],u∈[-1,0]时,恒有f(x)≥f(u),等号只在x=u=0时取到,故f(x)在[-1,1]上是增加的.
(3)由(2)知函数f(x)在(0,1)上递增,在[1,+∞)上递减,则f(x)在x=1处可取得最大值 .
∴f(1)=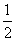 ,∴函数的最大值为
,∴函数的最大值为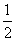 ,无最小值.
,无最小值.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 x|的定义域是[a,b],值域为[0,2],对于区间[m,n],称n-m为区间[m,n]的长度,则[a,b]长度的最小值为( )
x|的定义域是[a,b],值域为[0,2],对于区间[m,n],称n-m为区间[m,n]的长度,则[a,b]长度的最小值为( )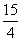 B.3
B.3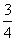
 若f(x0)≥2,则x0的取值范围是____________.
若f(x0)≥2,则x0的取值范围是____________. ] B.[
] B.[ +a是奇函数,则a=______.
+a是奇函数,则a=______.
 +y2=1,若函数y=f(x)的值域是(-1,1),则f(x)一定是( )
+y2=1,若函数y=f(x)的值域是(-1,1),则f(x)一定是( )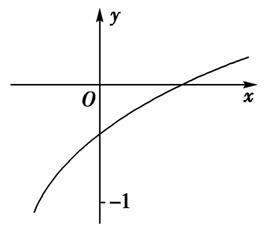
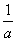 <b<1
<b<1 <a<1
<a<1