题目内容
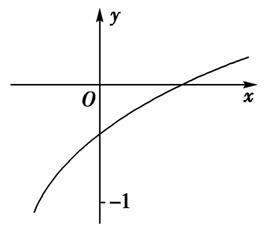
已知函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
A.0<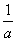 <b<1
<b<1
B.0<b<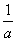 <1
<1
C.0< <a<1
<a<1
D.0<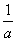 <
< <1
<1
A
[解析] 由图象知函数单调递增,所以a>1.
又-1<f(0)<0,
f(0)=loga(20+b-1)=logab,
即-1<logab<0,所以0<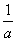 <b<1,故选A.
<b<1,故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )

A.0<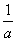 <b<1
<b<1
B.0<b<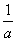 <1
<1
C.0< <a<1
<a<1
D.0<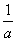 <
< <1
<1
A
[解析] 由图象知函数单调递增,所以a>1.
又-1<f(0)<0,
f(0)=loga(20+b-1)=logab,
即-1<logab<0,所以0<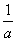 <b<1,故选A.
<b<1,故选A.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案