题目内容
7.在直三棱柱ABC-A1B1C1 中,∠ACB=90°,AA1=2,AC=BC=1,记A 1B1 的中点为E,平面C1 EC 与 AB1 C1 的交线为l,则直线l与 AC所成角的余弦值是( )| A. | $\frac{{\sqrt{6}}}{5}$ | B. | $\frac{{\sqrt{6}}}{4}$ | C. | $\frac{{\sqrt{6}}}{6}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
分析 取AB中点D,连结CD,ED,ED∩AB1=F,连结EF,则C1F即为平面C1 EC 与 AB1 C1 的交线l,以C 为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,利用利用向量法能求出直线l与 AC所成角的余弦值.
解答 解:取AB中点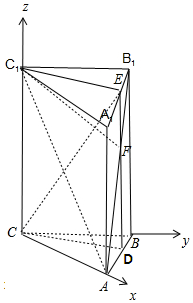 D,连结CD,ED,ED∩AB1=F,连结EF,
D,连结CD,ED,ED∩AB1=F,连结EF,
则C1F即为平面C1 EC 与 AB1 C1 的交线l,
以C 为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
则A(1,0,0),C(0,0,0),
C1(0,0,2),B1(0,1,2),F($\frac{1}{2},\frac{1}{2},1$),
$\overrightarrow{{C}_{1}F}$=($\frac{1}{2},\frac{1}{2},-1$),$\overrightarrow{CA}$=(1,0,0),
设直线l与 AC所成角为θ,
则cosθ=$\frac{|\overrightarrow{{C}_{1}F}•\overrightarrow{CA}|}{|\overrightarrow{{C}_{1}F}|•|\overrightarrow{CA}|}$=$\frac{\frac{1}{2}}{\sqrt{\frac{3}{2}}}$=$\frac{\sqrt{6}}{6}$.
∴直线l与 AC所成角的余弦值为$\frac{\sqrt{6}}{6}$.
故选:C.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
18.矩形ABCD中,AB=2,AD=1,在矩形ABCD的边CD上随机取一点E,记“△AEB的最大边是AB”为事件M,则P(M)等于( )
| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$-1 | C. | $\frac{2-\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
15.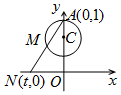 如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
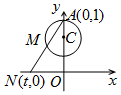 如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )| A. | 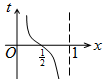 | B. | 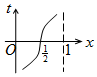 | C. | 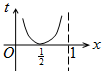 | D. | 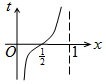 |
2.已知焦点在x 轴上的双曲线的渐近线方程为$y=±\frac{1}{2}x$,则双曲线的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
17.已知$f(x)=sin({x+\frac{π}{2}}),g(x)=cos({x-\frac{π}{2}})$,则下列结论中正确的是( )
| A. | 函数f(x)的图象向左平移π个单位长度可得到y=g(x)的函象 | |
| B. | 函数y=f(x)+g(x)的值域为[-2,2] | |
| C. | 函数y=f(x)•g(x)在$[{0,\frac{π}{2}}]$上单调递增 | |
| D. | 函数y=f(x)-g(x)的图象关于点$({\frac{π}{4},0})$对称 |