题目内容
19.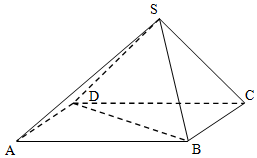 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.(1)求证:平面SAD⊥平面SBC;
(2)若BC=2,求点A到平面SBD的距离h的值.
分析 (1)证明:AD⊥SC,SA⊥SC,可得SC⊥平面SAD,即可证明平面SAD⊥平面SBC;
(2)利用等体积方法求点A到平面SBD的距离h的值.
解答  (1)证明:侧面SDC⊥底面ABCD,有AD⊥SC,AD⊥SD
(1)证明:侧面SDC⊥底面ABCD,有AD⊥SC,AD⊥SD
故△ADS为Rt△,有SD2+AD2=SA2
且AD=BC,SD=$\sqrt{2}$,故2+BC2=SA2
即BC2=SA2-2
连接AC,易得AC2=BC2+AB2=BC2+4
即BC2=AC2-4
那么SA2-2=AC2-4,整理后有AC2=SA2+2
又SC=$\sqrt{2}$,故AC2=SA2+SC2
所以△ASC为Rt△,有SA⊥SC
所以SC⊥平面SAD,那么平面SBC⊥平面SAD;
(2)解:由题意,BC⊥SC,SB=$\sqrt{6}$,DB=2$\sqrt{2}$,
∴DB2=SD2+SB2,∴SB⊥SD,
∴S△SBD=$\frac{1}{2}×\sqrt{2}×\sqrt{6}$=$\sqrt{3}$.
由等体积可得$\frac{1}{3}×\frac{1}{2}×2×2×1=\frac{1}{3}×\sqrt{3}×h$,∴h=$\frac{2\sqrt{3}}{3}$,
即点A到平面SBD的距离h的值为$\frac{2\sqrt{3}}{3}$.
点评 本题考查线面垂直的判定,考查平面与平面垂直的判定与性质,考查等体积方法的运用,属于中档题.

练习册系列答案
相关题目
7.某车间加工零件的数量x与加工时间y的统计数据如表:
现已求得如表数据的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\stackrel{∧}{b}$值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为102分钟.
| 零件数x(个) | 18 | 20 | 22 |
| 加工时间y(分钟) | 27 | 30 | 33 |
4.函数f(x)是定义在R上的奇函数,对任意两个不相等的正数x1,x2,都有$\frac{{x}_{2}f({x}_{1})-{x}_{1}f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,记a=-log23•f(log${\;}_{\frac{1}{3}}$2),b=f(1),c=4f(0.52),则( )
| A. | c<b<a | B. | b<a<c | C. | c<a<b | D. | a<b<c |
8.直线x-y-1=0的倾斜角与其在y轴上的截距分别是( )
| A. | 135°,1 | B. | 45°,-1 | C. | 45°,1 | D. | 135°,-1 |