题目内容
已知:AO⊥平面OBC,A-BC-O的平面角为α.求证:cosα=
.并类比平面直角三角形ABC(C为斜边),cosA=
.写出你的解题反思或解题感悟.
| S△OBC |
| S△ABC |
| a |
| c |
考点:类比推理
专题:空间角
分析:本题通过作出二面角的平面角,实现立体问题的平面化研究,从而降低了难度,将问题转化为平面内的问题,三角函数问题与面积问题,进行计算得到本题结论.反思类比的条件和结论,得到本题结论.
解答:
(1)证明:过点O作BC边所在直线的垂线,垂足为H,连结OH、AH,
∵AO⊥平面OBC,
∴AO⊥BC,
∵OH⊥BC,
∴BC⊥平面OAH,
∴BC⊥AH,
∴∠AHO为二面角A-BC-O的平面角,
∴∠AHO=α.
在△AOH中,cosα=cos∠AHO=
,
∵
=
=
,
∴cosα=
.
(2)在△AOH中,有cos∠AHO=
,
在空间四边形AOBC中,有cosα=
.
感悟:
两个结论的前提都是有垂直条件的存在,一个是在线线垂直条件下,一个是在线面垂直条件下,
结论是由平面图形拓展为立体图形,角由线线角拓展成了面面角,由线线比,拓展成了面积比.
另一方面,面是由线组成的,其结论与祖暅原理也在类似之处.
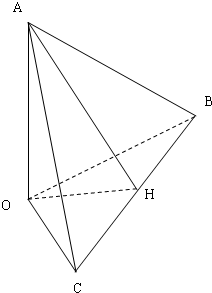
∵AO⊥平面OBC,
∴AO⊥BC,
∵OH⊥BC,
∴BC⊥平面OAH,
∴BC⊥AH,
∴∠AHO为二面角A-BC-O的平面角,
∴∠AHO=α.
在△AOH中,cosα=cos∠AHO=
| OH |
| AH |
∵
| S△OBC |
| S△ABC |
| ||
|
| OH |
| AH |
∴cosα=
| S△OBC |
| S△ABC |
(2)在△AOH中,有cos∠AHO=
| OH |
| AH |
在空间四边形AOBC中,有cosα=
| S△OBC |
| S△ABC |
感悟:
两个结论的前提都是有垂直条件的存在,一个是在线线垂直条件下,一个是在线面垂直条件下,
结论是由平面图形拓展为立体图形,角由线线角拓展成了面面角,由线线比,拓展成了面积比.
另一方面,面是由线组成的,其结论与祖暅原理也在类似之处.

点评:本题考查了立体几何的二面角的计算公式的证明,还考查了类比的思想,本题有一定的思维难度,有点开放性,属于好题.

练习册系列答案
相关题目
若一条直线与一个平面成72°角,则这条直线与这个平面内经过斜足的直线所成角中最大角等于( )
| A、72° | B、90° |
| C、108° | D、180° |
 如图,在空间四边形ABCD中,P、Q分别是△ABC和△BCD的重心,求证:PQ∥平面ACD.
如图,在空间四边形ABCD中,P、Q分别是△ABC和△BCD的重心,求证:PQ∥平面ACD.