题目内容
下列式子中成立的是(假定各式均有意义)( )
| A、logax•logay=loga(x+y) | |||||
| B、(logax)n=nlogax | |||||
C、
| |||||
D、
|
考点:对数的运算性质
专题:函数的性质及应用
分析:利用对数的运算法则进行判断,得到只有C正确.
解答:
解:logax•logay≠loga(x+y),故A错误;
(logax)n≠nlogax=logaxn,故B错误;
=loga
,由对数的运算法则知C正确;
≠logax-logay=loga
,故D错误.
故选:C.
(logax)n≠nlogax=logaxn,故B错误;
| logax |
| n |
| n | x |
| logax |
| logay |
| x |
| y |
故选:C.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意对数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将指数形式256=2x化为对数形式,下列结果正确的是( )
| A、log2256=8 |
| B、log2562=8 |
| C、log8256=2 |
| D、log2568=2 |
 某几何体的三视图如图所示,若其正视图为等腰梯形,侧视图为正三角形,则该几何体的表面积为( )
某几何体的三视图如图所示,若其正视图为等腰梯形,侧视图为正三角形,则该几何体的表面积为( )A、2
| ||
B、4
| ||
| C、6 | ||
| D、8 |
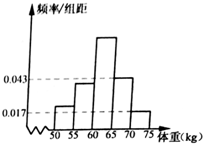 某校为了解2015届高三毕业班准备考飞行员学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右前3个小组的频率之比为1:2:4,其中第二小组的频率为11.
某校为了解2015届高三毕业班准备考飞行员学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右前3个小组的频率之比为1:2:4,其中第二小组的频率为11.