题目内容
已知关于x,y的方程
-m|x+2y-5|=0表示双曲线时,则m的取值范围为 .
| x2+y2-2x-16y+65 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:将方程变形,运用两点的距离公式和点到直线的距离公式,整理得到
m=
,再由双曲线的离心率的范围,解不等式即可得到.
| 5 |
| ||||
|
解答:
解:关于x,y的方程
-m|x+2y-5|=0,
即
=m|x+2y-5|,
则
m=
,
上式右边表示动点P(x,y)到定点F(1,8)的距离与定直线l:x+2y-5=0(F∉l)的距离之比,
由于方程表示双曲线,则
m>1,
解得,m>
.
故答案为:(
,+∞).
| x2+y2-2x-16y+65 |
即
| (x-1)2+(y-8)2 |
则
| 5 |
| ||||
|
上式右边表示动点P(x,y)到定点F(1,8)的距离与定直线l:x+2y-5=0(F∉l)的距离之比,
由于方程表示双曲线,则
| 5 |
解得,m>
| ||
| 5 |
故答案为:(
| ||
| 5 |
点评:本题考查双曲线的第二定义,考查离心率的范围,考查方程表示的几何意义,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
曲线C经过伸缩变换
后,对应曲线的方程为:x2+y2=1,则曲线C的方程为( )
|
A、
| ||||
B、4x2=
| ||||
C、
| ||||
| D、4x2+9y2=1 |
给出四个函数,分别满足①f(x+y)=f(x)+f(y),②g(x+y)=g(x)•g(y),③h(x•y)=h(x)+h(y),④m(x•y)=m(x)•m(y).又给出四个函数的图象,那么正确的匹配方案可以是( )
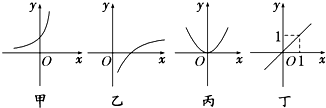

| A、①甲,②乙,③丙,④丁 |
| B、①乙,②丙,③甲,④丁 |
| C、①丙,②甲,③乙,④丁 |
| D、①丁,②甲,③乙,④丙 |
给定下列命题:
①全等的两个三角形面积相等;
②3的倍数一定能被6整除;
③如果ab=ac,那么b=c;
④若a<b,则a2<b2.
其中,真命题有( )
①全等的两个三角形面积相等;
②3的倍数一定能被6整除;
③如果ab=ac,那么b=c;
④若a<b,则a2<b2.
其中,真命题有( )
| A、① | B、①③④ |
| C、①④ | D、①②③④ |