题目内容
已知条件p:函数y=lg(-x2+8x+20)的定义域;条件q:{x|1-m≤x≤1+m,m>0},若¬p是¬q充分不必要条件,求实数m的取值范围.
考点:必要条件、充分条件与充要条件的判断,命题的否定
专题:简易逻辑
分析:求出函数的定义域,得到p,转化命题的否定命题,利用充分不必要条件列出关系式即可求解m的范围.
解答:
解:由-x2+8x+20>0可得p:A={-2<x<10}
因为若¬p是¬q充分不必要条件,所以q是p的充分不必要条件
由于q:B={x|1-m≤x≤1+m,m>0}
所以B?A,由
解得0<m<3.
因为若¬p是¬q充分不必要条件,所以q是p的充分不必要条件
由于q:B={x|1-m≤x≤1+m,m>0}
所以B?A,由
|
解得0<m<3.
点评:本题考查充要条件以及命题真假的应用,考查基本知识的应用以及转化思想.

练习册系列答案
相关题目
已知集合M{x|x2-x>0},N={0,1,2,3},则(∁UM)∩N=( )
| A、{x|0≤x≤1} |
| B、{0,1} |
| C、{2,3} |
| D、{1,2,3} |
(
)
,53,(
)-2的大小关系是( )
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 3 |
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
已知集合A={1,2,0,-2},B={0,2,4},则A∩B=( )
| A、{1,-2} |
| B、{0,2} |
| C、{0,1,2,4,-2} |
| D、{1,-2,4} |
已知cos(
+α)=-
,且α为第四象限角,则cos(-3π+α)=( )
| 3π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
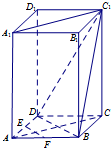 在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.
在长方体ABCD-A1B1C1D1中,底面ABCD为正方形,E,F分别为棱AD、,AB的中点.