题目内容
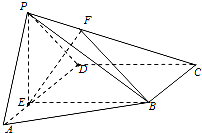 如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2
如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2| 3 |
(1)已知
| PF |
| PC |
(2)求证:CB⊥面PEB,并求点D到面PBC的距离.
考点:直线与平面垂直的性质,直线与平面平行的判定
专题:计算题,证明题,空间位置关系与距离
分析:(1)连接AC交BE于点M,连接FM,运用线面平行的性质定理,得到PA∥FM,再由平行线分线段成比例,得到
λ的值;
(2)先求出PE=
,从而PE⊥AD,再由面面垂直的性质定理,以及线面垂直的判定定理,即可证得CB⊥面PEB,设点D到面PBC的距离为d,由VD-PBC=VP-DBC,运用棱锥的体积公式,即可求得.
λ的值;
(2)先求出PE=
| 3 |
解答:
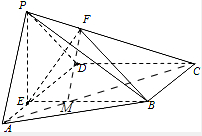 (1)解:连接AC交BE于点M,连接FM,
(1)解:连接AC交BE于点M,连接FM,
∵PA∥面BEF,FM=面PAC∩面BEF,∴PA∥FM,
∵EM∥CD,∴
=
=
,
∵PA∥FM,∴
=
=
.
∵
=λ
(λ∈R),
∴λ=
;
(2)∵AP=2,AE=1,∠PAD=60°,
∴PE=
,∴PE⊥AD
又面PAD⊥面ABCD,且面PAD∩面ABCD=AD,∴PE⊥面ABCD
∴PE⊥CB
又∴BE⊥CB,且∴PE∩BE=E,∴CB⊥面PEB,
设点D到面PBC的距离为d,由VD-PBC=VP-DBC,
得
×
×2×2
×d=
×
×2×3×
,
求得d=
.
 (1)解:连接AC交BE于点M,连接FM,
(1)解:连接AC交BE于点M,连接FM,∵PA∥面BEF,FM=面PAC∩面BEF,∴PA∥FM,
∵EM∥CD,∴
| AM |
| MC |
| AE |
| ED |
| 1 |
| 2 |
∵PA∥FM,∴
| PF |
| FC |
| AM |
| MC |
| 1 |
| 2 |
∵
| PF |
| PC |
∴λ=
| 1 |
| 3 |
(2)∵AP=2,AE=1,∠PAD=60°,
∴PE=
| 3 |
又面PAD⊥面ABCD,且面PAD∩面ABCD=AD,∴PE⊥面ABCD
∴PE⊥CB
又∴BE⊥CB,且∴PE∩BE=E,∴CB⊥面PEB,
设点D到面PBC的距离为d,由VD-PBC=VP-DBC,
得
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
求得d=
| 3 |
| 2 |
点评:本题考查线面平行的性质定理和线面垂直的判定和性质定理,面面垂直的性质定理,同时考查等积法求点到平面的距离,平行线分线段成比例等,属于中档题.

练习册系列答案
相关题目