题目内容
已知函数f(x)=x+
(1)用函数单调性的定义证明f(x)在区间[1,+∞)上为增函数
(2)解不等式f(x2-2x+2)>f(5)
| 1 |
| x |
(1)用函数单调性的定义证明f(x)在区间[1,+∞)上为增函数
(2)解不等式f(x2-2x+2)>f(5)
考点:函数单调性的性质,函数的单调性及单调区间
专题:函数的性质及应用
分析:(1)任取区间[1,+∞)上两个实数a,b,且a<b,判断f(a)-f(b)的符号,进而得到f(a),f(b)的大小,根据单调性的定义即可得到答案.
(2)由(1)中结论及x2-2x+2≥1,可将不等式f(x2-2x+2)>f(5)化为:x2-2x+2>5,解得不等式的解集.
(2)由(1)中结论及x2-2x+2≥1,可将不等式f(x2-2x+2)>f(5)化为:x2-2x+2>5,解得不等式的解集.
解答:
解:(1)证明:任取区间[1,+∞)上两个实数a,b,且a<b
则a-b<0,ab>1,ab-1>0
则f(a)-f(b)=(a+
)-(b+
)
=a-b+
-
=a-b+
=(a-b)(1-
)=
<0
即f(a)<f(b)
故函数f(x)=x+
在区间[1,+∞)上是增函数略 (6分)
(2)x2-2x+2≥1,所以不等式f(x2-2x+2)>f(5)可化为:
x2-2x+2>5
解得:x∈(-∞,-1)∪(3,+∞)(12分)
则a-b<0,ab>1,ab-1>0
则f(a)-f(b)=(a+
| 1 |
| a |
| 1 |
| b |
=a-b+
| 1 |
| a |
| 1 |
| b |
| b-a |
| ab |
| 1 |
| ab |
| (a-b)(ab-1) |
| ab |
即f(a)<f(b)
故函数f(x)=x+
| 1 |
| x |
(2)x2-2x+2≥1,所以不等式f(x2-2x+2)>f(5)可化为:
x2-2x+2>5
解得:x∈(-∞,-1)∪(3,+∞)(12分)
点评:本题考查的知识点是函数的单调性的判断与证明,利用定义法(作差法)证明单调性的步骤是:设元→作差→分解→断号→结论.

练习册系列答案
相关题目
 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示.观察图形,回答下列问题: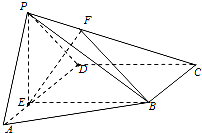 如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2
如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2