题目内容

两等差数列{an}和{bn}，前n项和分别为Sn，Tn，且
Sn
Tn
=
7n+2
n+3
，则
a2+a20
b7+b15
等于
 
．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用
a2+a20
b7+b15
=
21
2
(a1+a21)
21
2
(b1+b21)
=
S21
T21
，即可得出结论．
解答： 解：
a2+a20
b7+b15
=
21
2
(a1+a21)
21
2
(b1+b21)
=
S21
T21
=
7×21+2
21+3
=
149
24
．
故答案为：
149
24
．
点评：本题考查等差数列的性质与求和公式的运用，比较基础．
练习册系列答案
相关题目
在△ABC中，AB=2，AC=3，A=60°，则cosB=
 
．
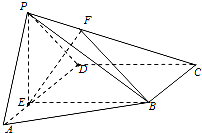如图，在四棱锥P-ABCD中，E为AD上一点，面PAD⊥面ABCD，四边形BCDE为矩形∠PAD=60°，PB=2
3
，PA=ED=2AE=2．
（1）已知
PF
=λ
PC
（λ∈R），且PA∥面BEF，求λ的值；
（2）求证：CB⊥面PEB，并求点D到面PBC的距离．
若某几何体的三视图如图，该几何体的体积为2，则俯视图中的x=
 
抛物线y2=2px（p＞0）的焦点为F，已知点A，B为抛物线上的两个动点，且满足∠AFB=120°．过弦AB的中点M作抛物线准线的垂线MN，垂足为N，则
|MN|
|AB|
的最大值为
 
．
将函数y=
1
2x+1
的图象沿x轴向左平移2个单位后，得到图象C，则C的图象对应的函数解析式为
 
．
已知离心率为2的双曲线
x2
m
+
y2
n
=1（m，n∈R）的右焦点与抛物线y2=4x的焦点重合，则
m
n
=
 
．
关于函数f（x）=4sin（2x+
π
3
）（x∈R），有下列论断：
①函数y=f（x）的表达式可改写为y=4cos（2x-
π
6
）；
②函数y=f（x）的最小正周期为2π；
③函数y=f（x）的图象关于点（-
π
6
，0）对称；
④函数y=f（x）的图象可由y=4sin2x向左平移
π
3
个单位得到；
⑤函数y=f（x）在区间[-
11π
12
，-
5π
12
）上单调递减．
其中正确的是
 
．（将你认为正确的论断的序号都填上）
已知|
OA
|=1，|
OB
|=k，∠AOB=
2π
3
，点C在∠AOB内，
OC
•
OA
=0，若
OC
=2m
OA
+m
OB
，|
OC
|=2
3
，则k=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网