题目内容
下列命题:
①在一个2×2列联表中,由计算得k2=6.679,则有99%的把握确认这两个变量间有关系
②若二项式(x+
)n的展开式中所有项的系数之和为243,则展开式中x-4的系数是40
③随机变量X服从正态分布N(1,2),则P(X<0)=P(X>2)
④若正数x,y满足2x+y-3=0,则
的最小值为3
其中正确命题的序号为 .
①在一个2×2列联表中,由计算得k2=6.679,则有99%的把握确认这两个变量间有关系
②若二项式(x+
| 2 |
| x2 |
③随机变量X服从正态分布N(1,2),则P(X<0)=P(X>2)
④若正数x,y满足2x+y-3=0,则
| x+2y |
| xy |
其中正确命题的序号为
考点:命题的真假判断与应用
专题:阅读型,概率与统计,二项式定理
分析:①在一个2×2列联表中,由计算得K2=6.679>6.535,则有99%的把握确认这两个变量间有关系.
②令x=1,则3n=243,n=5,求出通项公式,并化简,再令x的次数为-4,求出系数即可;
③由正态分布密度曲线关于直线x=1对称,即可判断;
④
=
+
=
(2x+y)(
+
),展开合并,再运用基本不等式,即可求出最小值,注意等号成立的条件.
②令x=1,则3n=243,n=5,求出通项公式,并化简,再令x的次数为-4,求出系数即可;
③由正态分布密度曲线关于直线x=1对称,即可判断;
④
| x+2y |
| xy |
| 2 |
| x |
| 1 |
| y |
| 1 |
| 3 |
| 2 |
| x |
| 1 |
| y |
解答:
解:①在一个2×2列联表中,由计算得K2=6.679>6.535,则有99%的把握确认这两个变量间有关系,①正确;
②令x=1,则3n=243,n=5,通项为
•x5-r•(
)r=
•2r•x5-3r,令5-3r=-4,则r=3,则
展开式中x-4的系数是
•23=80.故②错;
③随机变量X服从正态分布N(1,2),由正态分布密度曲线关于直线x=1对称,则P(X<0)=P(X>2),故③对;
④若正数x,y满足2x+y-3=0,即有2x+y=3,则
=
+
=
(2x+y)(
+
)=
(5+
+
)
≥
×(5+2
)=3.当且仅当x=y=1取最小值3.故④对.
故答案为:①③④
②令x=1,则3n=243,n=5,通项为
| C | r 5 |
| 2 |
| x2 |
| C | r 5 |
展开式中x-4的系数是
| C | 3 5 |
③随机变量X服从正态分布N(1,2),由正态分布密度曲线关于直线x=1对称,则P(X<0)=P(X>2),故③对;
④若正数x,y满足2x+y-3=0,即有2x+y=3,则
| x+2y |
| xy |
| 2 |
| x |
| 1 |
| y |
| 1 |
| 3 |
| 2 |
| x |
| 1 |
| y |
| 1 |
| 3 |
| 2y |
| x |
| 2x |
| y |
≥
| 1 |
| 3 |
| 4 |
故答案为:①③④
点评:本题考查正态分布曲线的特点,随机变量的相关性,考查二项式定理的运用求系数,以及应用基本不等式求最值,注意等号成立的条件,属于比较基础的题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
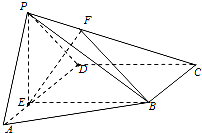 如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2
如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形BCDE为矩形∠PAD=60°,PB=2