题目内容
14.已知$α∈(\frac{π}{2},π)$,$sinα=\frac{4}{5}$,则sin2α=( )| A. | $-\frac{24}{25}$ | B. | $-\frac{7}{25}$ | C. | $\frac{7}{25}$ | D. | $\frac{24}{25}$ |
分析 由已知利用同角三角函数基本关系式可求cosα,利用二倍角公式即可得解.
解答 解:∵$α∈(\frac{π}{2},π)$,$sinα=\frac{4}{5}$,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{3}{5}$,
∴sin2α=2sinαcosα=2×$\frac{4}{5}$×(-$\frac{3}{5}$)=-$\frac{24}{25}$.
故选:A.
点评 本题主要考查了同角三角函数基本关系式,二倍角公式在三角函数化简求值中的应用,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
5.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2$\sqrt{3}$,则|$\overrightarrow{a}$|=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | 3 |
9.已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则图中阴影部分的集合为( )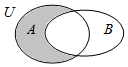

| A. | {x|-1<x<1} | B. | {x|1≤x<3} | C. | {x|x<3} | D. | {x|x≤-1} |
19.复数z=$\frac{2}{1+i}$(i是虚数单位)的共轭复数在复平面内对应的点是( )
| A. | (1,1) | B. | (1,-1) | C. | (-1,1) | D. | (-1,-1) |
3.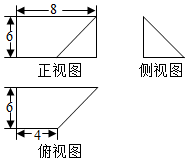 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )| A. | 72 | B. | 80 | C. | 120 | D. | 144 |