题目内容
13．四棱锥P-ABCD的底面ABCD为正方形，PA⊥底面ABCD，AB=2，若该四棱锥的所有顶点都在同一球面上，且该球的表面积为$\frac{81π}{4}$，则该棱锥的高为（ ）| A． | $\frac{7}{2}$ | B． | $\frac{7}{4}$ | C． | 2$\sqrt{2}$ | D． | $\sqrt{2}$ |
分析 利用条件确定球的直径，利用勾股定理，即可求棱锥的高．
解答 解：可以将四棱锥P-ABCD补成球的内接长方体，其对角线PC即为球的直径．
∵球的表面积为$\frac{81π}{4}$，
∴球的半径为$\frac{9}{4}$，
设PA=x，则PC的长等于$\sqrt{4+4+{x}^{2}}$=$\frac{81}{4}$，即x=$\frac{7}{2}$．
故选：A．
点评 本题主要考查球的表面积公式，构造长方体是解决本题的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
10．某商品销量q与售价p满足q=10-λp，总成本c与销量满足c=4+μq，销售收入r与售价及销量之间满足r=pq，其中λ，μ均为正常数，设利润=销售收入-总成本，则利润最大时的售价为（ ）
| A． | $\frac{10-λμ}{λ}$ | B． | $\frac{10+λμ}{λ}$ | C． | $\frac{10-λμ}{2λ}$ | D． | $\frac{10+λμ}{2λ}$ |
4．已知函数f1（x）=$\frac{lg（1-{x}^{2}）}{|{x}^{2}-2|-2}$；f2（x）=（x-1）•$\sqrt{\frac{x+1}{x-1}}$；f3（x）=loga（x+$\sqrt{{x}^{2}+1}$），（a＞0，a≠1）；f4（x）=x•（$\frac{1}{{2}^{x}-1}+\frac{1}{2}$），（x≠0），下面关于这四个函数奇偶性的判断正确的是（ ）
| A． | 都是偶函数 | |
| B． | 一个奇函数，一个偶函数，两个非奇非偶函数 | |
| C． | 一个奇函数，两个偶函数，一个非奇非偶函数 | |
| D． | 一个奇函数，三个偶函数 |
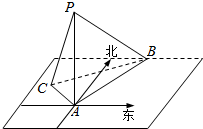如图所示，在海岛A上有一座海拔$\sqrt{3}$千米的山峰上，山顶上设有一座观察站P，一艘轮船沿一固定方向匀速航行，上午10：00时，测得此船在岛北偏东20°且俯角为30°的B处，到10：10时，又测得该船在岛北偏西40°且俯角为60°的C处，则该船的航行速度为$6\sqrt{7}$千米/时．
18．下列函数中，在其定义域内是增函数而且又是奇函数的是（ ）
| A． | y=2x | B． | y=2|x| | C． | y=2x-2-x | D． | y=2x+2-x |