题目内容
如果f(x)=
,那么f[f(2)]= .
|
考点:函数的值
专题:计算题,函数的性质及应用
分析:先求出f(2)的值,从而求出f[f(2)]的值.
解答:
解:∵f(2)=sin2<1,
∴f(sin2)=1,
故答案为:1.
∴f(sin2)=1,
故答案为:1.
点评:本题考查了分段函数问题,考查了函数求值问题,是一道基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
若函数f(x)=x-
(a∈R)在区间(1,2)上有零点,则a的值可能是( )
| a |
| x |
| A、-2 | B、0 | C、1 | D、3 |
已知
,
,
表示共面的三个单位向量,
⊥
,那么(
+
)•(
+
)的取值范围是( )
| i |
| j |
| k |
| i |
| j |
| i |
| k |
| j |
| k |
| A、[-3,3] | ||||
| B、[-2,2] | ||||
C、[
| ||||
D、[1-
|
对于定义在实数集R上的函数f(x),若f(x)与f(x+1)都是偶函数,则( )
| A、f(x)是奇函数 |
| B、f(x-1)是奇函数 |
| C、f(x+2)是偶函数 |
| D、f(x+3)是奇函数 |
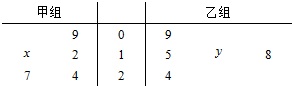 以下茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).
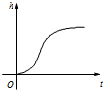
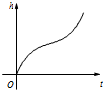
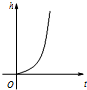
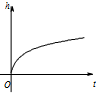
以下茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).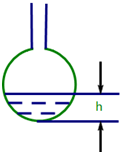 匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )
匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )