题目内容
已知等比数列an=
,其前n项和为Sn=
ak,则Sk+1与Sk的递推关系不满足( )
| 1 |
| 3n-1 |
| n |
 |
| k-1 |
A、Sk+1=Sk+
| ||
B、Sk+1=1+
| ||
| C、Sk+1=Sk+ak+1 | ||
| D、Sk+1=3Sk-3+ak+ak+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件,求出数列{an}的通项公式和前n项和公式,由此利用数列的性质进行运算,能得到Sk+1与Sk的递推关系.
解答:
解:∵等比数列an=
=31-n,
∴a1=1,a2=
,q=
,
∴Sn=
ak=
=
(1-
),
∴Sk+1=Sk+
,故A不成立;
Sk+1=
(1-
)=
-
×
=1+
-
×
=1+
(1-
)=1+
Sk,故B成立;
由数列的前n项和的定义知:Sk+1=Sk+ak+1,故C成立;
∵3Sk-3+ak+ak+1
=3×
(1-
)-3+31-k+3-k
=
-
×
-3+
+
=
-
×
=
(1-
)=Sk+1,故D成立.
故选A.
| 1 |
| 3n-1 |
∴a1=1,a2=
| 1 |
| 3 |
| 1 |
| 3 |
∴Sn=
| n |
 |
| k=1 |
1-
| ||
1-
|
| 3 |
| 2 |
| 1 |
| 3n |
∴Sk+1=Sk+
| 1 |
| 3k |
Sk+1=
| 3 |
| 2 |
| 1 |
| 3n |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3n |
=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3n-1 |
=1+
| 1 |
| 2 |
| 1 |
| 3n-1 |
| 1 |
| 3 |
由数列的前n项和的定义知:Sk+1=Sk+ak+1,故C成立;
∵3Sk-3+ak+ak+1
=3×
| 3 |
| 2 |
| 1 |
| 3k-1 |
=
| 9 |
| 2 |
| 9 |
| 2 |
| 1 |
| 3n-1 |
| 1 |
| 3k-1 |
| 3 |
| 3k-1 |
=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3k-1 |
=
| 3 |
| 2 |
| 1 |
| 3k |
故选A.
点评:本题考查数列的通项公式和前n项和的应用,是中档题,解题时要注意通项公式和前n项和间的等价转化.

练习册系列答案
相关题目
抛物线y2=2px(p>0)的焦点为F,已知点A,B为抛物线上的两个动点,且满足∠AFB=90°.过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则
的最大值为( )
|
| ||
|
|
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
 某几何体的三视图如图所示,其中俯视图是个半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中俯视图是个半圆,则该几何体的体积为( )A、
| ||||
| B、π | ||||
C、
| ||||
D、
|
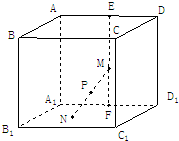 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AD,A1D1的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A1B1C1D1上运动,则线段MN的中点P在二面角A-A1D1-B1内运动所形成的轨迹(曲面)的面积为( )
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AD,A1D1的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A1B1C1D1上运动,则线段MN的中点P在二面角A-A1D1-B1内运动所形成的轨迹(曲面)的面积为( )| A、4π | ||
| B、π | ||
C、
| ||
| D、2π |
直线x+
y-2=0被圆(x-1)2+y2=1所截得的弦长为( )
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |