题目内容
某工厂共有10台机器,生产一种仪器元件,由于受生产能力和技术水平等因素限制,会产生一定数量的次品.根据经验知道,每台机器产生的次品数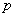 (万件)与每台机器的日产量
(万件)与每台机器的日产量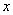 (万件)
(万件)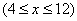 之间满足关系:
之间满足关系: 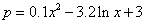 .已知每生产1万件合格的元件可以盈利2万元,但每产生1万件次品将亏损1万元.(利润=盈利—亏损)
.已知每生产1万件合格的元件可以盈利2万元,但每产生1万件次品将亏损1万元.(利润=盈利—亏损)
(1)试将该工厂每天生产这种元件所获得的利润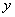 (万元)表示为
(万元)表示为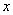 的函数;
的函数;
(2)当每台机器的日产量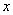 (万件)为多少时所获得的利润最大,最大利润为多少?
(万件)为多少时所获得的利润最大,最大利润为多少?
解析】(1)由题意可得所获得的利润为:



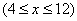 .
.
(2)∵
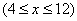 ,
,
∴
 ,
,
令 ,解得
,解得 或
或 (舍去),
(舍去),
当 时,
时, ,当
,当 时,
时, ,
,
∴函数在 上为增函数,在
上为增函数,在 为减函数,
为减函数,
∴当 时,函数取得极大值,即当
时,函数取得极大值,即当 时,获得最大利润,最大利润为
时,获得最大利润,最大利润为
 (万元),
(万元),
答: 当每台机器的日产量 万件时,获得利润最大,最大利润为
万件时,获得利润最大,最大利润为 万元.
万元.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 的方程
的方程 的两根均在区间
的两根均在区间 内,求
内,求 的范围.
的范围. ,则
,则 的最小值是( )
的最小值是( ) B.
B. C.
C. D.
D.
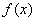 的定义域为开区间
的定义域为开区间 ,导函数
,导函数 在
在 个 B.
个 B. 个 C.
个 C. 个 D.
个 D. 个
个
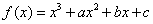 (实数
(实数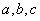 为常数)的图象过原点, 且在
为常数)的图象过原点, 且在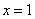 处的切线为直线
处的切线为直线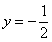 .(1)求函数
.(1)求函数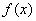 的解析式;(2)若常数
的解析式;(2)若常数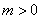 ,求函数
,求函数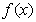 在区间
在区间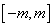 上的最大值.
上的最大值.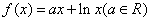 .
. 的单调区间;(2)设
的单调区间;(2)设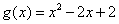 ,若对任意
,若对任意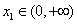 ,均存在
,均存在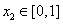 ,使得
,使得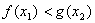 ,求
,求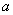 的取值范围.
的取值范围. ;
; .(1)求曲线在点
.(1)求曲线在点 处的切线方程;(2)求曲线过点
处的切线方程;(2)求曲线过点 的曲线的切线方程.
的曲线的切线方程. 满足
满足 ,
, ,求
,求 .
.