Question

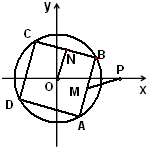如图，已知点P（2，0），正方形ABCD内接于圆O：x²+y²=2，M，N分别为边AB，BC的中点．则当正方形ABCD绕圆心O旋转时，

PM

•

ON

的取值范围为

 

．

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：首先，根据

OM

⊥

ON

，设M（cosα，sinα），N（-sinα，cosα），然后，写出向量

PM

=（cosα-2，sinα）和

ON

=（-sinα，cosα），从而得到

PM

•

ON

=2sinα，进而确定其范围．

解答： 解：设M（cosα，sinα），
∵

OM

⊥

ON

，
∴

OM

•

ON

=0，
∴N（-sinα，cosα），
∴

ON

=（-sinα，cosα），

OM

=（cosα，sinα），
∴

PM

=（cosα-2，sinα），
∴

PM

•

ON

=-sinα（cosα-2）+sinαcosα=2sinα，
∵sinα∈[-1，1]，
∴2sinα∈[-2，2]，
∴

PM

•

ON

的取值范围是[-2，2]．
故答案为：[-2，2]

点评：本题重点考查了平面向量的实际运用，重点掌握平面向量的坐标运算等知识，属于中档题．