题目内容
函数f(x)=x2+ax-3的图象与x轴在区间(1,2)上仅有一个交点,则实数a的取值范围为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:由题意可得要满足题意只需f(1)<0且f(2)>0即可,解不等式组可得.
解答:
解:∵函数f(x)=x2+ax-3的图象过定点(0,-3),
且函数图象为开口向上的抛物线,
要满足题意只需f(1)<0且f(2)>0即可,
∴a-2<0且2a+1>0,解得-
<a<2
故答案为:(-
,2)
且函数图象为开口向上的抛物线,
要满足题意只需f(1)<0且f(2)>0即可,
∴a-2<0且2a+1>0,解得-
| 1 |
| 2 |
故答案为:(-
| 1 |
| 2 |
点评:本题考查二次函数的性质,属基础题.

练习册系列答案
相关题目
椭圆C:
+
=1(a>b>0)的两个焦点为F1,F2,M为椭圆上一点,且
•
的最大值的取值范围是[c2,2c2],其中c是椭圆的半焦距,则椭圆的离心率取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| MF1 |
| MF2 |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
椭圆
+
=1的内接矩形的最大面积是( )
| x2 |
| 36 |
| y2 |
| 9 |
| A、36 | B、18 | C、54 | D、40 |
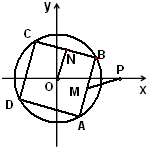 如图,已知点P(2,0),正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点.则当正方形ABCD绕圆心O旋转时,
如图,已知点P(2,0),正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点.则当正方形ABCD绕圆心O旋转时,