题目内容
在极坐标系中,经过点A(5,0)垂直于极轴的直线的极坐标方程是( )
| A、x=5 |
| B、ρcosθ=5 |
| C、ρsinθ=5 |
| D、ρsinθ=-5 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:由题意可得,所求直线的直角坐标方程为x=5,再根据x=ρcosθ化为极坐标方程.
解答:
解:由题意可得,所求直线的直角坐标方程为x=5,化为极坐标方程可得 ρcosθ=5,
故选:B.
故选:B.
点评:本题主要考查把直角坐标方程化为极坐标方程的方法,利用了公式x=ρcosθ,属于基础题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知a,b,c∈R+,满足abc(a+b+c)=1,则S=(a+c)(b+c)的最小值为( )
| A、1 | B、2 | C、3 | D、4 |
椭圆
+
=1的内接矩形的最大面积是( )
| x2 |
| 36 |
| y2 |
| 9 |
| A、36 | B、18 | C、54 | D、40 |
若C
=C
,则n的值为( )
2 n |
6 n |
| A、11 | B、10 | C、9 | D、8 |
二维空间中,圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2;三维空间中,球的二维测度(表面积)S=4πr2,三维测度(体积)V=
πr3.应用合情推理,若四维空间中,“超球”的三维测度V=8πr3,则其四维测度W=( )
| 4 |
| 3 |
| A、2πr4 |
| B、3πr4 |
| C、4πr4 |
| D、6πr4 |
已知直角三角形的两条直角边长分别为4和6,则这两直角边上的中线所夹的锐角的余弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
极坐标方程4sin2θ=3表示曲线是 ( )
| A、两条射线 | B、抛物线 |
| C、圆 | D、两条相交直线 |
一个书包内装有5本不同的小说,另一书包内有6本不同学科的教材,从两个书包中各取一本书的取法共有( )
| A、5种 | B、6种 |
| C、11种 | D、30种 |
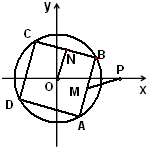 如图,已知点P(2,0),正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点.则当正方形ABCD绕圆心O旋转时,
如图,已知点P(2,0),正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点.则当正方形ABCD绕圆心O旋转时,