题目内容
已知实数x,y满足
,则z=2x+y的最大值为( )
|
| A、14 | B、12 | C、6 | D、3 |
考点:简单线性规划
专题:不等式的解法及应用
分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件画出满足约束条件
的可行域,再用角点法,求出目标函数的最大值.
|
解答:
解:满足约束条件
的可行域如下图中阴影部分所示:
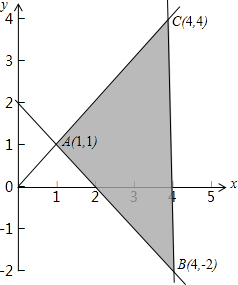
∵目标函数Z=2x+y,
∴ZA=3,ZB=6,ZC=12,
故Z=2x+y的最大值是12,
故选:B
|

∵目标函数Z=2x+y,
∴ZA=3,ZB=6,ZC=12,
故Z=2x+y的最大值是12,
故选:B
点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
椭圆C:
+
=1(a>b>0)的两个焦点为F1,F2,M为椭圆上一点,且
•
的最大值的取值范围是[c2,2c2],其中c是椭圆的半焦距,则椭圆的离心率取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| MF1 |
| MF2 |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
在执行如图所示的程序框图时,若输入8、9、6、5、4、8、7、6、10,则输出的S=( )


| A、9 | ||
| B、7 | ||
C、
| ||
D、
|
给出命题p:f(x)=sinx+
cosx的周期为π;命题q:若数列{an}前n项和Sn=n2+2n,则数列{an}为等差数列,则下列四个命题“p且q”,“p或q”,“非p”,“非q”中,真命题个数为( )
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
已知a,b,c∈R+,满足abc(a+b+c)=1,则S=(a+c)(b+c)的最小值为( )
| A、1 | B、2 | C、3 | D、4 |
椭圆
+
=1的内接矩形的最大面积是( )
| x2 |
| 36 |
| y2 |
| 9 |
| A、36 | B、18 | C、54 | D、40 |
极坐标方程4sin2θ=3表示曲线是 ( )
| A、两条射线 | B、抛物线 |
| C、圆 | D、两条相交直线 |
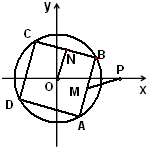 如图,已知点P(2,0),正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点.则当正方形ABCD绕圆心O旋转时,
如图,已知点P(2,0),正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点.则当正方形ABCD绕圆心O旋转时,