题目内容
8.已知数列{an}与{bn}满足an+1-an=q(bn+1-bn),n∈N*(1)若bn=2n-3,a1=1,q=2,求数列{an}的通项公式;
(2)若a1=1,b1=2,且数列{bn}为公比不为1的等比数列,求q的值,使数列{an}也是等比数列;
(3)若a1=q,bn=qn(n∈N*),且q∈(-1,0),数列{an}有最大值M与最小值m,求$\frac{M}{m}$的取值范围.
分析 (1)由bn=2n-3,可得bn+1-bn=2.又a1=1,q=2,可得an+1-an=4,再利用等差数列的通项公式即可得出;
(2)由于数列{bn}是公比为k不为1的等比数列,b1=2.可得bn=2•kn-1.利用an+1-an=q(bn+1-bn),a1=1.可得a2,a3,再利用${a}_{2}^{2}$=a1a3,即可得出.
(3)由于a1=q,bn=qn(n∈N*),可得an+1-an=qn+2-qn+1.利用“累加求和”可得:an=qn+1+q-q2,利用q∈(-1,0),可得:q3≤qn+1≤q2,再利用基本不等式的性质即可得出.
解答 解:(1)∵bn=2n-3,∴bn+1-bn=2.
又a1=1,q=2,
∴an+1-an=q(bn+1-bn)=2×2=4,
∴数列{an}是等差数列,首项为1,公差为4.
∴an=1+4(n-1)=4n-3.
(2)∵数列{bn}是公比为k不为1的等比数列,b1=2.
∴bn=2•kn-1.
∵an+1-an=q(bn+1-bn),a1=1.
∴a2=1+q(2k-2),
同理可得:a3=a2+q(b3-b2)=1+q(2k-2)+q(2k2-2k),
∵${a}_{2}^{2}$=a1a3,
∴[1+q(2k-2)]2=1×[1+q(2k-2)+q(2k2-2k)],k≠1.
化为2q=1或q=0,解得q=$\frac{1}{2}$或q=0.
(3)∵a1=q,bn=qn(n∈N*),
∴an+1-an=q(qn+1-qn)=qn+2-qn+1.
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(qn+1-qn)+(qn-qn-1)+…+(q3-q2)+q
=qn+1+q-q2,
∵q∈(-1,0),
∴qn+1∈(-1,1),q3≤qn+1≤q2,
∴数列{an}有最大值M=q,最小值m=q3-q2+q.
∴$\frac{M}{m}$=$\frac{q}{{q}^{3}-{q}^{2}+q}$=$\frac{1}{{q}^{2}-q+1}$=$\frac{1}{(q-\frac{1}{2})^{2}+\frac{3}{4}}$∈$(\frac{1}{3},1)$.
点评 本题考查了数列的通项公式、等比数列与等差数列的通项公式及其前n项和公式、“累加求和”、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案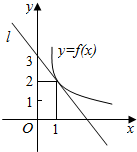 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,令h(x)=xf(x),h′(x)是h(x)的导函数,则h′(1)的值是( )| A. | 2 | B. | 1 | C. | -1 | D. | $\frac{1}{2}$ |
| A. | 1-3i | B. | 1+3i | C. | $\frac{1}{2}$-$\frac{3}{2}$i | D. | $\frac{1}{2}$+$\frac{3}{2}$i |
| A. | c>a>b | B. | c>b>a | C. | a>b>c | D. | b>a>c |
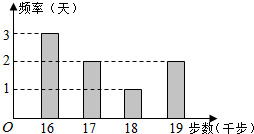 小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:| 健步走步数(前步) | 16 | 17 | 18 | 19 |
| 消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(Ⅱ)从步数为17千步,18千步,19千步的几天中任选2天,求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率.
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |
 已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,交半圆于点E,DE=1
已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,交半圆于点E,DE=1