题目内容
若α为锐角，且sin（
-α）=
，则sinα= ．
| π |
| 3 |
| 1 |
| 3 |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：由已知中α为锐角，且sin（
-α）=
，先求出cos（
-α），进而根据sinα=sin[
-（
-α）]=sin
cos（
-α）-cos
sin（
-α）得到答案．
| π |
| 3 |
| 1 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：
解：∵α为锐角，
∴
-α∈（-
，
），
又∵sin（
-α）=
＞0，
故
-α∈（0，
）．
∴cos（
-α）=
=
，
∴sinα=sin[
-（
-α）]=sin
cos（
-α）-cos
sin（
-α）=
×
-
×
=
，
故答案为：
∴
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
又∵sin（
| π |
| 3 |
| 1 |
| 3 |
故
| π |
| 3 |
| π |
| 3 |
∴cos（
| π |
| 3 |
1-(
|
2
| ||
| 3 |
∴sinα=sin[
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
2
| ||
| 6 |
故答案为：
2
| ||
| 6 |
点评：本题考查的知识点是两角和与差的正弦函数，同角三角函数的基本关系，其中sinα=sin[
-（
-α）]的转化是解答的关键．
| π |
| 3 |
| π |
| 3 |
练习册系列答案
名校课堂系列答案
相关题目
如图四棱锥P-ABCD的底面是矩形，PA⊥平面ABCD，E、F分别是AB、PD的中点，又二面角P-CD-B为45°
某校400名学生今年高考数学分数的频率分布直方图如图，则这400名学生中，分数在[90，110）之间的有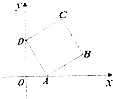
如图，边长为1的正方形ABCD的顶点A，D分别在x轴，y轴正半轴上移动，则